NN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
21 tháng 10 2017
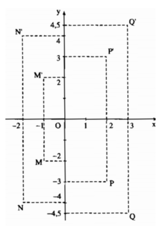
Gọi M’, N’, P’, Q’ là các điểm lần lượt đối xứng qua các điểm M, N, P, Q qua trục Ox, ta thấy rằng hoành độ của các điểm đối xứng nhau qua trục hoành bằng nhau, còn tung độ của các điểm đó thì đối nhau: M’(-1; 2); N’(-2; 4); P’(2; 3); Q’(3; 4,5).
15 tháng 11 2023
a: B đối xứng A qua trục tung Oy
=>\(\left\{{}\begin{matrix}x_B=-x_A=-2\\y_B=y_A=1\end{matrix}\right.\)
Vậy: B(-2;1)
b: C đối xứng A qua trục Ox
=>\(\left\{{}\begin{matrix}x_C=x_A=2\\y_C=-y_A=-1\end{matrix}\right.\)
Vậy: C(2;-1)
c: D đối xứng A qua O
=>O là trung điểm của AD
=>\(\left\{{}\begin{matrix}x_A+x_D=0\\y_A+y_D=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_D=-x_A=-2\\y_D=-y_A=-1\end{matrix}\right.\)
Vậy: D(-2;-1)
d: (d): y=2x-1
=>(d): 2x-y-1=0
E đối xứng A qua (d)
=>(d) là đường trung trực của AD
Gọi (d2): ax+by+c=0 là phương trình đường thẳng AD
(d) là trung trực của AD
=>(d) vuông góc (d2) tại trung điểm của AD(1) và (d2) đi qua A(2;1)
(d): 2x-y-1=0
=>(d2): x+2y+c=0
Thay x=2 và y=1 vào (d2), ta được:
\(c+2+2\cdot1=0\)
=>c=-4
=>(d2): x+2y-4=0
Tọa độ giao điểm F của (d) với (d2) là:
\(\left\{{}\begin{matrix}x+2y-4=0\\2x-y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\2x-y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=8\\2x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=7\\x+2y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{7}{5}\\x=4-2y=4-\dfrac{14}{5}=\dfrac{6}{5}\end{matrix}\right.\)
(1) suy ra F là trung điểm của AE
=>\(\left\{{}\begin{matrix}\dfrac{6}{5}=\dfrac{x_A+x_E}{2}=\dfrac{2+x_E}{2}\\\dfrac{7}{5}=\dfrac{y_A+y_E}{2}=\dfrac{y_E+1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_E+2=\dfrac{12}{5}\\y_E+1=\dfrac{14}{5}\end{matrix}\right.\Leftrightarrow E\left(\dfrac{2}{5};\dfrac{9}{5}\right)\)
CH
Cô Hoàng Huyền
Admin
VIP
29 tháng 6 2017
Cô hướng dẫn nhé. Do tính chất đối xứng, ta suy ra AB = BD; AM = MI hay BM là đường trung bình tam giác ADI.
Từ đó ta có BM // DI và DI = 2BM.
Hoàn toàn tương tự : MC // IE và IE = 2MC
Lại có MB = MC và B, M, C thẳng hàng nên D, I, E thẳng hàng và DI = IE
Vậy D đối xứng với E qua I.
A'(4;-4)
a*(4;-4)