Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\dfrac{-36}{63};\dfrac{56}{63};\dfrac{-30}{63}\)
b)\(\dfrac{110}{264};\dfrac{21}{264}\)

a ,mẫu số chung nhỏ nhất là 35
b,mẫu số chung nhỏ nhất là 75
c,mẫu số chung nhỏ nhất là 24
a ,mẫu số chung nhỏ nhất là 35
b,mẫu số chung nhỏ nhất là 75
c,mẫu số chung nhỏ nhất là 24

Sửa lại đề:
\(M=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+....+\dfrac{1}{49.50}\)
\(M=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-..........-\dfrac{1}{49}-\dfrac{1}{50}\)
\(M=1-\dfrac{1}{50}\)
\(M=\dfrac{50}{50}-\dfrac{1}{50}\)
\(M=\dfrac{49}{50}\)
Đề bài là thu gọn / tính giá trị biểu thức nhé chứ không phải là So sánh , thiếu dữ kiện kìa

Giải: Ta có: \(\dfrac{1}{2.3}\)=\(\dfrac{1}{2}-\dfrac{1}{3}\) ; \(\dfrac{1}{2}-\dfrac{1}{3}\)(giữ nguyên)
Vì \(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1}{2}-\dfrac{1}{3}\) nên \(\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
Vậy \(\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)

1)Tính
a)\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+..........+\dfrac{1}{9.10}\)
=\(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+.....+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=1-\dfrac{1}{10}\)
\(=\dfrac{9}{10}\)
b)\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+.........+\dfrac{1}{99.100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+..............+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}\)
\(=\dfrac{99}{100}\)
2) tìm x
\(a\)) \(\dfrac{2}{5}+\dfrac{4}{5}x-\dfrac{7}{5}\)\(=\dfrac{9}{5}\)
\(\dfrac{4}{5}x+\dfrac{7}{5}=\dfrac{9}{5}-\dfrac{2}{5}\)
\(\dfrac{4}{5}x+\dfrac{7}{5}=\dfrac{7}{5}\)
\(\dfrac{4}{5}x=\dfrac{7}{5}-\dfrac{7}{5}\)
\(\dfrac{4}{5}x=0\)
\(x=0:\dfrac{4}{5}\)
\(x=0\)
b)\(\dfrac{2}{5}x-\dfrac{6}{4}=\dfrac{8}{5}\)
\(\dfrac{2}{5}x=\dfrac{8}{5}+\dfrac{6}{4}\)
\(\dfrac{2}{5}x=\dfrac{31}{10}\)
\(x=\dfrac{31}{10}:\dfrac{2}{5}\)
\(x=\dfrac{31}{4}\)
1. Tính:
a. \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\)
= \(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
= \(\dfrac{1}{1}-\dfrac{1}{10}\)
= \(\dfrac{10}{10}-\dfrac{1}{10}\)
= \(\dfrac{9}{10}\)
b. \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)
= \(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
= \(\dfrac{1}{1}-\dfrac{1}{100}\)
= \(\dfrac{100}{100}-\dfrac{1}{100}\)
= \(\dfrac{99}{100}\)
2. Tìm x, biết:
a. \(\dfrac{2}{5}+\dfrac{4}{5}x-\dfrac{7}{5}=\dfrac{9}{5}\)
\(\dfrac{4}{5}x-\dfrac{7}{5}=\dfrac{9}{5}-\dfrac{2}{5}\)
\(\dfrac{4}{5}x-\dfrac{7}{5}=\dfrac{7}{5}\)
\(\dfrac{4}{5}x=\dfrac{7}{5}+\dfrac{7}{5}\)
\(\dfrac{4}{5}x=\dfrac{14}{5}\)
\(x=\dfrac{14}{5}:\dfrac{4}{5}\)
\(x=\dfrac{14}{5}.\dfrac{5}{4}\)
\(x=14.\dfrac{1}{4}\)
\(x=\dfrac{14}{4}\)
Vậy \(x=\dfrac{14}{4}\)
b. \(\dfrac{2}{5}x-\dfrac{6}{4}=\dfrac{8}{5}\)
\(\dfrac{2}{5}x=\dfrac{8}{5}+\dfrac{6}{4}\)
\(\dfrac{2}{5}x=\dfrac{32}{20}+\dfrac{30}{20}\)
\(\dfrac{2}{5}x=\dfrac{62}{20}\)
\(\dfrac{2}{5}x=\dfrac{31}{10}\)
\(x=\dfrac{31}{10}:\dfrac{2}{5}\)
\(x=\dfrac{31}{10}.\dfrac{5}{2}\)
\(x=\dfrac{31}{2}.\dfrac{2}{2}\)
\(x=\dfrac{31}{2}.1\)
\(x=\dfrac{31}{2}\)
Vậy \(x=\dfrac{31}{2}\)
bài này mk tự làm ko sao chép trên mạng![]()
nếu thấy đúng thì tick đúng cho mk nha![]()

\(\dfrac{2}{1.2}+\dfrac{2}{2.3}+\dfrac{2}{3.4}+...............+\dfrac{2}{2008.2009}\)
\(=2\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+................+\dfrac{1}{2008.2009}\right)\)
\(=2\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+.................+\dfrac{1}{2008}-\dfrac{1}{2009}\right)\)
\(=2\left(1-\dfrac{1}{2009}\right)\)
\(=2.\dfrac{2008}{2009}=\dfrac{4016}{2009}\)

\(A=\dfrac{3^{10}\cdot11+3^{10}\cdot5}{3^9\cdot2^4}=\dfrac{3^{10}\cdot\left(11+5\right)}{3^9\cdot16}=\dfrac{3^{10}\cdot16}{3^9\cdot16}=3\)
\(B=\dfrac{2^{10}\cdot13+2^{10}\cdot65}{2^8\cdot104}=\dfrac{2^{10}\cdot\left(13+65\right)}{2^8\cdot2^2\cdot26}=\dfrac{2^{10}\cdot78}{2^{10}\cdot26}=3\)
\(C=\dfrac{72^3\cdot54^2}{108^4}=\dfrac{\left(2^3\cdot3^2\right)^3\cdot\left(2\cdot3^3\right)^2}{\left(3^3\cdot2^2\right)^4}\\ =\dfrac{2^9\cdot3^6\cdot2^4\cdot3^6}{3^{12}\cdot2^8}=\dfrac{2^{13}\cdot3^{12}}{3^{12}\cdot2^8}=2^5=32\)
\(D=\dfrac{11\cdot3^{22}\cdot3^7-9^{15}}{\left(2\cdot3^{14}\right)^2}=\dfrac{11\cdot3^{29}-\left(3^2\right)^{15}}{2^2\cdot3^{28}}=\dfrac{11\cdot3^{29}-3^{30}}{2^2\cdot3^{28}}\\ =\dfrac{3^{29}\cdot\left(11-3\right)}{2^2\cdot3^{28}}=\dfrac{3^{29}\cdot8}{4\cdot3^{28}}=3\cdot2=6\)

a: \(B=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2007}-\dfrac{1}{2008}=1-\dfrac{1}{2008}=\dfrac{2007}{2008}\)
b: \(Q=\dfrac{7}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2009\cdot2011}\right)\)
\(=\dfrac{7}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\)
\(=\dfrac{7}{2}\cdot\dfrac{2010}{2011}\simeq3,50\)
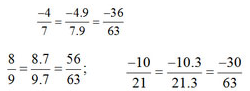
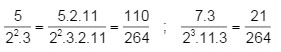
SAI THÌ THÔI
BCNN=36
\(\dfrac{5}{36}=\dfrac{5}{36}>0>-\dfrac{7}{12}\)