
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{-5}{6}.\dfrac{120}{25}< x< \dfrac{-7}{15}.\dfrac{9}{14}\)
\(\Rightarrow-4< x< \dfrac{-3}{10}\)
\(\Rightarrow\dfrac{-40}{10}< x< \dfrac{-3}{10}\)
\(\Rightarrow x\in\left\{\dfrac{-39}{10};\dfrac{-38}{10};\dfrac{-37}{10};...;\dfrac{-5}{10};\dfrac{-4}{10}\right\}\)
b) \(\left(\dfrac{-5}{3}\right)^2< x< \dfrac{-24}{35}.\dfrac{-5}{6}\)
\(\Rightarrow\dfrac{25}{9}< x< \dfrac{4}{7}\)
\(\Rightarrow\dfrac{175}{63}< x< \dfrac{36}{63}\)
\(\Rightarrow x=\varnothing\)
c) \(\dfrac{1}{18}< \dfrac{x}{12}< \dfrac{y}{9}< \dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{2}{36}< \dfrac{3x}{36}< \dfrac{4y}{36}< \dfrac{9}{36}\)
\(\Rightarrow x\in\left\{1;2\right\}\)
+) Với \(x=1\)
\(\Rightarrow y\in\left\{1;2\right\}\)
+) Với \(x=2\)
\(\Rightarrow y=2\)
Vậy \(x=1\) thì \(y\in\left\{1;2\right\}\); \(x=2\) thì \(y=8\).

a)\(\dfrac{3}{10}\)-x=\(\dfrac{25}{30}\)-\(\dfrac{4}{30}\)
\(\dfrac{3}{10}-x=\dfrac{7}{10}\)
x = \(\dfrac{3}{10}-\dfrac{7}{10}\)
x=\(\dfrac{-4}{10}\)
b)\(\dfrac{-5}{8}+x=\dfrac{4}{9}-\dfrac{63}{9}\)
\(\dfrac{-5}{9}+x=\dfrac{-59}{9}\)
\(x=\dfrac{-59}{9}-\dfrac{-5}{9}\)
\(x=\dfrac{-64}{9}\)
c)=>2.18=(x-3).(x-3)
=>36=(x-3)\(^2\)
=>6\(^2\)=(x-3)\(^2\)
6= x-3
x=6+3=9

a,Vì \(\dfrac{5}{6}\)=\(\dfrac{x}{24}\) nên ta có: 5.24:6= 20 \(\Rightarrow\)x =20
Mấy câu sau làm tương tự như vậy.
b,x =21
c,x =9
d,x = -5

a: \(=\dfrac{-28}{36}+\dfrac{15}{36}-\dfrac{26}{36}=\dfrac{-39}{36}=\dfrac{-13}{12}\)
b: \(=\dfrac{11}{9}\left(\dfrac{15}{4}-\dfrac{7}{4}-\dfrac{5}{4}\right)=\dfrac{11}{9}\cdot\dfrac{3}{4}=\dfrac{11}{12}\)
c: \(=15+\dfrac{9}{7}+6+\dfrac{2}{3}-5-\dfrac{5}{9}\)
\(=16+\dfrac{88}{63}=\dfrac{1096}{63}\)
d: \(=\dfrac{5}{6}-\dfrac{1}{3}+\dfrac{2}{18}\)
\(=\dfrac{15-6+2}{18}=\dfrac{11}{18}\)

a , \(\left(\dfrac{-2}{3}+1\dfrac{1}{4}-\dfrac{1}{6}\right):\dfrac{-24}{10}\)
=\(\left(\dfrac{-2}{3}+\dfrac{5}{4}-\dfrac{1}{6}\right):\dfrac{-12}{5}\)
=\(\left(\dfrac{-8}{12}+\dfrac{15}{12}-\dfrac{2}{12}\right)\cdot\dfrac{-5}{12}\)
=\(\dfrac{5}{12}\cdot\dfrac{-5}{12}=\dfrac{-25}{144}\)
b , \(\dfrac{13}{15}\cdot0,25\cdot3+\left(\dfrac{8}{15}-1\dfrac{19}{60}\right)1\dfrac{23}{24}\)
=\(\dfrac{13}{15}\cdot\dfrac{1}{4}\cdot3+\left(\dfrac{8}{15}-\dfrac{79}{60}\right)\cdot\dfrac{57}{24}\)
=\(\dfrac{13}{20}-\dfrac{47}{60}\cdot\dfrac{57}{24}\)
=\(\dfrac{13}{20}-\dfrac{893}{480}=\dfrac{312}{480}-\dfrac{893}{480}=\dfrac{-581}{480}\)
c , \(\left(\dfrac{12}{32}+\dfrac{5}{-20}-\dfrac{10}{24}\right):\dfrac{2}{3}\)
=\(\left(\dfrac{180}{480}-\dfrac{120}{480}-\dfrac{200}{480}\right)\cdot\dfrac{3}{2}\)
= \(\dfrac{-7}{24}\cdot\dfrac{3}{2}=\dfrac{-7}{16}\)
d , \(4\dfrac{1}{2}:\left(2,5-3\dfrac{3}{4}\right)+\left(-\dfrac{1}{2}\right)\)
=\(\dfrac{9}{2}:\left(\dfrac{5}{2}-\dfrac{15}{4}\right)-\dfrac{1}{2}\)
=\(\dfrac{9}{2}:\dfrac{-5}{4}-\dfrac{1}{2}=\dfrac{9}{2}\cdot\dfrac{-4}{5}-\dfrac{1}{2}=\dfrac{-18}{5}-\dfrac{1}{2}=\dfrac{-41}{10}\)
e , \(\dfrac{-5}{2}:\left(\dfrac{3}{4}-\dfrac{1}{2}\right)=\dfrac{-5}{2}\left(\dfrac{3}{4}-\dfrac{2}{4}\right)\)
=\(\dfrac{-5}{2}:\dfrac{1}{4}=\dfrac{-5}{2}\cdot4=-10\)

b) \(\dfrac{7x-21}{14x-42}=\dfrac{2}{4}\)
\(\Leftrightarrow\dfrac{7\left(x-3\right)}{14\left(x-3\right)}=\dfrac{2}{4}\)
Ở tử và mẫu đều có chung x-3 nên loại
\(\Rightarrow\dfrac{7}{14}=\dfrac{2}{4}\Leftrightarrow\dfrac{2}{4}=\dfrac{2}{4}\) (đpcm)
c) \(\dfrac{9x-18}{18y-54}=\dfrac{2x-4}{4y-12}\)
\(\Leftrightarrow\dfrac{9\left(x-2\right)}{18\left(y-3\right)}=\dfrac{2\left(x-2\right)}{4\left(y-3\right)}\)
Ở tử VT và VP đều có tử là x-2 và mẫu là y-3 nên loại
\(\Leftrightarrow\dfrac{9}{18}=\dfrac{2}{4}\Leftrightarrow\dfrac{1}{2}=\dfrac{1}{2}\) (đpcm)

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)

Đề răng dài thế này thì tui giải từng câu hí
a) \(\dfrac{-7}{9}+\dfrac{5}{12}-\dfrac{13}{18}\left(MSC:36\right)\)
\(=\dfrac{-28}{36}+\dfrac{15}{36}-\dfrac{26}{36}\)
\(=\dfrac{-13}{36}-\dfrac{26}{36}\)
\(=\dfrac{-39}{36}\)
\(=\dfrac{13}{3}\)
b) \(\dfrac{11}{9}.\dfrac{15}{4}-\dfrac{11}{4}.\dfrac{7}{9}-\dfrac{11}{9}.\dfrac{5}{4}\)
\(=\left(\dfrac{15}{4}-\dfrac{11}{4}-\dfrac{5}{4}\right).\dfrac{11}{9}\)
\(=\left(1-\dfrac{5}{4}\right).\dfrac{11}{9}\)
\(=\left(\dfrac{4}{4}-\dfrac{5}{4}\right).\dfrac{11}{9}\)
\(=\dfrac{-1}{4}.\dfrac{11}{9}\)
\(=\dfrac{-11}{36}\)

b)
\(\dfrac{3}{y}< \dfrac{y}{7}\)
\(\Rightarrow21< y^2\)
\(\dfrac{y}{7}< \dfrac{4}{y}\Rightarrow y^2< 28\)
=> \(21< y^2< 28\)
=> y = 5
c)
\(\dfrac{1}{8}< \dfrac{x}{18}\Rightarrow48< 8x\Rightarrow x>6\)
\(\dfrac{y}{24}< \dfrac{2}{9}\Rightarrow9y< 48\Rightarrow y< 5\)
Lại có
\(\dfrac{x}{18}< \dfrac{y}{24}\Rightarrow24x< 18y\Rightarrow4x< 3y\) (1)
Mà x > 6 ; y < 5 (2)
=> (1) và (2) mâu thuẫn => không có giá trị x , y cần tìm
\( b) \dfrac{3}{y} < \dfrac{y}{7} < \dfrac{4}{y} \)
=>21/4y<y^2/4y<28/4y
=>21<y^2<28
Do \(y^2\) là số chính phương ,21<y^2<28=>y^2=25<=>y=5
Vậy \(y=5\)
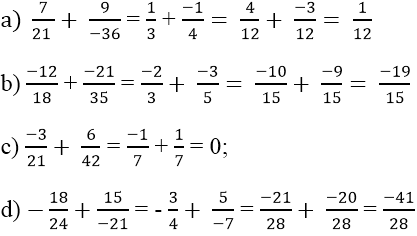
\(\dfrac{4}{x-6}=\dfrac{y}{24}=-\dfrac{12}{18}\)
\(x-6=\dfrac{4\cdot18}{-12}=-6\)
\(\Rightarrow x=0\)
\(y=\dfrac{24\cdot\left(-12\right)}{18}=-16\)
`4/(x-6)=(-12)/18`
`=>4/(x-6)=(-2)/3`
`=>2/(x-6)=-1/3`
`=>x-6=-6`
`=>x=0`
`y/24=(-12)/48=(-2)/3`
`=>3y=24=>y=8`
Vậy `x=0,y=8`