Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a.\(12,5.\left(-\dfrac{5}{7}\right)+1,5.\left(-\dfrac{5}{7}\right)\)
\(=\left(-\dfrac{5}{7}\right).\left(12,5+1,5\right)\)
\(=-10\)
b,\(\left(-\dfrac{2}{5}-\dfrac{3}{7}\right):\dfrac{4}{5}+\left(-\dfrac{1}{5}+\dfrac{3}{7}\right):\dfrac{4}{5}\)
\(=\left(-\dfrac{2}{5}-\dfrac{3}{7}-\dfrac{1}{5}+\dfrac{3}{7}\right):\dfrac{4}{5}\)
\(=-\dfrac{3}{5}:\dfrac{4}{5}\)
\(=-\dfrac{3}{4}\)
c,\(12.\left(-\dfrac{2}{3}\right)^2+\dfrac{4}{3}\)
\(=12.\dfrac{4}{9}+\dfrac{4}{3}\)
\(=\dfrac{16}{3}+\dfrac{4}{3}\)
\(=\dfrac{20}{3}\)
d,\(1:\left(\dfrac{2}{3}-\dfrac{3}{4}\right)^2\)
\(=\dfrac{1}{1}:\dfrac{1}{144}\)
\(=144\)
e,\(15.\left(-\dfrac{2}{3}\right)^2-\dfrac{7}{3}\)
\(=15.\dfrac{4}{9}-\dfrac{7}{3}\)
\(=\dfrac{20}{3}-\dfrac{7}{3}\)
\(=\dfrac{13}{3}\)
a) = ( 12,5 +1,5 ). \(\left(-\dfrac{5}{7}\right)\)
= 14 . \(\left(-\dfrac{5}{7}\right)\)
= -10
b) = (\(-\dfrac{2}{5}+-\dfrac{1}{5}\)) + \(\left(\dfrac{3}{7}-\dfrac{3}{7}\right)\): \(\dfrac{4}{5}\)
= \(\left(-\dfrac{3}{5}+0\right)\): \(\dfrac{4}{5}\)
= \(\dfrac{3}{4}\)
c) = \(\left(12.-\dfrac{2}{9}\right)\) + \(\dfrac{4}{3}\)
= \(\dfrac{8}{3}\) + \(\dfrac{4}{3}\)
= \(-\dfrac{4}{3}\)
d) = 1: \(\dfrac{23}{48}\)
=\(\dfrac{48}{23}\)
e) =\(\left(15.-\dfrac{2}{9}\right)-\dfrac{7}{3}\)
= \(\left(-\dfrac{10}{3}\right)-\dfrac{7}{3}\)
=\(-\dfrac{17}{3}\)
f) = 10 485.76
a) \(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2=\left(\dfrac{13}{14}\right)^2=\dfrac{169}{196}\)
b) \(\left(\dfrac{3}{4}-\dfrac{5}{6}\right)^2=\left(\dfrac{-1}{12}\right)^2=\dfrac{1}{144}\)
c) \(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{\left(5.20\right)^4}{\left(25.4\right)^5}=\dfrac{100^4}{100^5}=\dfrac{1}{100}\)
d) \(\left(\dfrac{-10}{3}\right)^5.\left(\dfrac{-6}{5}\right)^4=\dfrac{-10^5}{3^5}.\dfrac{-6^4}{5^4}=\dfrac{-\left(2.5\right)^5.\left(3.2\right)^4}{3^5.5^4}=\dfrac{-29.5}{3}=-853\dfrac{1}{3}\)
Toàn câu dễ nên bạn tự làm đi.
Trong lúc bạn đánh xong bài này thì bạn có thể làm xong rồi đó.
Đừng có ỷ lại vào người khác ,động não lên.
2: \(=\dfrac{203}{60}\cdot\dfrac{81}{1225}=\dfrac{783}{3500}\)
= 
= 
= 
= 
. 
a) \(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2=\left(\dfrac{6}{14}+\dfrac{7}{17}\right)^2=\left(\dfrac{13}{12}\right)^2=\dfrac{13^2}{12^2}=\dfrac{169}{144}\)
b)\(\left(\dfrac{3}{4}-\dfrac{5}{6}\right)^2=\left(\dfrac{9}{12}-\dfrac{10}{12}\right)^2=\left(\dfrac{-1}{12}\right)^2=\dfrac{\left(-1\right)^2}{12^2}=\dfrac{1}{144}\)
c)\(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{5^4.5^4.2^8}{5^{10}.2^{10}}=\dfrac{5^8.2^8}{5^8.5^2.2^8.2^2}=\dfrac{1}{5^2.2^2}=\dfrac{1}{25.4}=\dfrac{1}{100}\)
d)\(\left(\dfrac{-10}{3}\right)^5.\left(\dfrac{-6}{5}\right)^4=\dfrac{\left(-10\right)^5.\left(-6\right)^4}{3^5.5^4}=\dfrac{\left(-2\right)^5.5^5.2^4.3^4}{3^4.3.5^4}=\dfrac{\left(-2\right)^5.5.5^42^4}{3.5^4}=\dfrac{\left(-2\right)^5.5.2^4}{3}=\dfrac{-2560}{3}=-853\dfrac{1}{3}\)
Câu 2:
\(B=\dfrac{5^{21}\cdot\left(2\cdot5-9\right)}{5^{20}}\cdot\dfrac{7^{15}\left(7+3\right)}{15\cdot7^{15}-95\cdot7^{14}}\)
\(=\dfrac{5\cdot1}{1}\cdot\dfrac{7^{15}\cdot10}{7^{14}\cdot\left(15\cdot7-95\right)}\)
\(=5\cdot\dfrac{7\cdot10}{105-95}=5\cdot7=35\)
a) \(\left(1,25\right)^3.8^3=\left(1,25.8\right)^3=1000\)
b) \(\left(\dfrac{-11}{9}\right)^4.\left(\dfrac{27}{22}\right)^4=\left(\dfrac{-11}{9}.\dfrac{27}{22}\right)^4=\left(\dfrac{-11.9.3}{9.2.\left(-11\right)}\right)^4\)
\(=\left(\dfrac{3}{2}\right)^4=\dfrac{81}{16}\)
c) \(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2=\left(\dfrac{13}{14}\right)^2=\dfrac{169}{196}\)
d) \(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{\left(5.20\right)^4}{\left(25.4\right)^5}=\dfrac{100^4}{100^5}=100^{-1}=0,01\)
Em chuyển hỗn số thành phân số theo CT(\(a\dfrac{b}{c}=\dfrac{a.c+b}{c}\)) tính trong ngoặc trước rồi nhân phân số theo CT: (\(\dfrac{a}{b}.\dfrac{c}{d}=\dfrac{a.c}{b.d}\)) nha.
câu 1 \(A=\dfrac{3^2}{5^2}.5^2-\dfrac{9^3}{4^3}:\dfrac{3^3}{4^3}+\dfrac{1}{2}\)
\(A=\dfrac{3^2}{5^2}.5^2-\dfrac{\left(3^2\right)^3}{4^3}.\dfrac{4^3}{3^3}+\dfrac{1}{2}\)
\(A=\dfrac{3^2}{5^2}.5^2-\dfrac{3^6}{4^3}.\dfrac{4^3}{3^3}+\dfrac{1}{2}=3^2-3^3+\dfrac{1}{2}=-18+\dfrac{1}{2}=-\dfrac{35}{2}\)
\(B=\left[\dfrac{4}{11}+\dfrac{7}{22}.2\right]^{2010}-\left(\dfrac{1}{2^2}.\dfrac{4^4}{8^2}\right)^{2009}\)
\(B=\left[\dfrac{4}{11}+\dfrac{7}{11}\right]^{2010}-\left(\dfrac{1}{2^2}.\dfrac{\left(2^2\right)^4}{\left(2^3\right)^2}\right)^{2009}\)
\(B=1^{2010}-\left(\dfrac{1}{2^2}.\dfrac{2^8}{2^6}\right)^{2009}\)
\(B=1^{2010}-\left(\dfrac{2^8}{2^8}\right)^{2009}\)
\(B=1^{2010}-1^{2009}=1-1=0\)
câu 2
a) \(2x-\dfrac{5}{4}=\dfrac{20}{15}\)
\(\Leftrightarrow2x=\dfrac{4}{3}+\dfrac{5}{4}\)
\(\Leftrightarrow2x=\dfrac{31}{12}\)
\(\Leftrightarrow x=\dfrac{31}{24}\)
b) \(\left(x+\dfrac{1}{3}\right)^3=\left(-\dfrac{1}{2}\right)^3\)
\(\Leftrightarrow x+\dfrac{1}{3}=-\dfrac{1}{2}\)
\(\Leftrightarrow x=-\dfrac{1}{2}-\dfrac{1}{3}\)
\(\Leftrightarrow x=-\dfrac{5}{6}\)
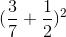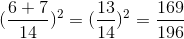
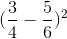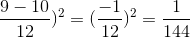
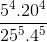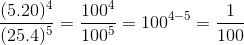
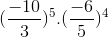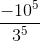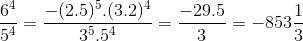
\(=\dfrac{3^5\cdot2^4\cdot5^4\cdot7^5}{7^5\cdot5^4\cdot3^4\cdot5^2\cdot4^2}=\dfrac{3^5}{3^4}\cdot\dfrac{5^4}{5^4\cdot5^2}\cdot\dfrac{2^4}{2^4}=\dfrac{3}{5^2}=\dfrac{3}{25}\)