Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\frac{4}{3.5}+\frac{4}{5.7}+...+\frac{4}{97.99}\)
\(=4.\left(\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{97.99}\right)\)
\(=4.\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{97}-\frac{1}{99}\right)\)
\(=4.\left(\frac{1}{3}-\frac{1}{99}\right)\)
\(=4.\frac{32}{99}\)
\(=\frac{128}{99}\)
\(\frac{4}{3.5}+\frac{4}{5.7}+...+\frac{4}{97.99}\)
\(=2\left(\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{97.99}\right)\)
\(=2\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{97}-\frac{1}{99}\right)\)
\(=2\left(\frac{1}{3}-\frac{1}{99}\right)\)
\(=2.\frac{32}{99}\)
\(=\frac{64}{99}\)

=6.3/2.5 +6.3/5.8+...+6.3/203.206
=6(3/2.5+3/5.8+...+3/203.206)
=6(1/2-1/5+1/5-1/8+...+1/203-1/206)
=6[(1/2-1/206)+(1/5-1/5)+(1/8-1/8)+...+(1/203-1/203)]
=6(1/2-1/206)=6(103/206-1/206)=6. 102/206=6. 51/103=306/103
A=6.( 3/2.5+3/5.8+...+3/203.206)
=6.(1/2-1/5+1/3-1/8+...+1/202-1/206)
=6.(1/2-1/206)=306/103

7)\(\dfrac{-19}{34}\left(\dfrac{17}{19}+\dfrac{49}{18}\right)+\dfrac{49}{18}\left(\dfrac{19}{34}-\dfrac{18}{7}\right)\)
=\(\dfrac{-19}{34}.\dfrac{17}{19}+\dfrac{49}{18}.\dfrac{-19}{34}+\dfrac{49}{18}.\dfrac{19}{34}-\dfrac{18}{7}.\dfrac{49}{18}\)
=\(\dfrac{1}{2}+\left(\dfrac{49}{18}.\dfrac{-19}{34}+\dfrac{49}{18}.\dfrac{19}{34}\right)-7\)
=\(\dfrac{1}{2}+\left[\dfrac{49}{18}\left(\dfrac{-19}{34}+\dfrac{19}{34}\right)\right]-7\)
=\(\dfrac{1}{2}+0-7=\dfrac{-13}{2}\)
8)\(\dfrac{29}{32}\left(\dfrac{41}{36}-\dfrac{32}{58}\right)-\dfrac{41}{36}\left(\dfrac{29}{32}+\dfrac{18}{41}\right)\)
=\(\dfrac{29}{32}.\dfrac{41}{36}-\dfrac{29}{32}.\dfrac{32}{58}-\dfrac{41}{36}.\dfrac{29}{32}+\dfrac{18}{41}.\dfrac{41}{36}\)
=\(\left(\dfrac{29}{32}.\dfrac{41}{36}-\dfrac{41}{36}\dfrac{29}{32}\right)-\dfrac{29}{32}.\dfrac{32}{58}+\dfrac{18}{41}.\dfrac{41}{36}\)
=\(0-\dfrac{1}{2}+\dfrac{1}{2}=0\)

1.
a) \(\dfrac{5}{18}+\dfrac{4}{7}+\dfrac{13}{18}+\dfrac{3}{7}\)
\(=\left(\dfrac{5}{18}+\dfrac{13}{18}\right)+\left(\dfrac{4}{7}+\dfrac{3}{7}\right)\)
\(=1+1=2\)
b) \(\dfrac{4}{9}.\dfrac{5}{19}.\dfrac{9}{4}\)
\(=\left(\dfrac{4}{9}.\dfrac{9}{4}\right).\dfrac{5}{19}\)
\(=1.\dfrac{5}{19}=\dfrac{5}{19}\)
tik mik nha!!!
2) \(\dfrac{4}{9}.\dfrac{5}{19}.\dfrac{9}{4} =(\dfrac{4}{9}.\dfrac{9}{4}).\dfrac{5}{19} =1.\dfrac{5}{19} =\dfrac{5}{19}\)

A = \(\dfrac{4}{2.5}\) + \(\dfrac{4}{5.8}\) + \(\dfrac{4}{8.11}\) + ... + \(\dfrac{4}{65.68}\)
7A = \(\dfrac{4.3}{2.5}\) + \(\dfrac{4.3}{5.8}\) + \(\dfrac{4.3}{8.11}\) + ... + \(\dfrac{4.3}{65.68}\)
7A = 4 (\(\dfrac{3}{2.5}\) + \(\dfrac{3}{5.8}\) + \(\dfrac{3}{8.11}\) + ... + \(\dfrac{3}{65.68}\))
7A = 4 (\(\dfrac{1}{2}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{8}\) + \(\dfrac{1}{8}\) - \(\dfrac{1}{11}\) + ... + \(\dfrac{1}{65}\) - \(\dfrac{1}{68}\))
7A = 4 (\(\dfrac{1}{2}\) - \(\dfrac{1}{68}\))
7A = 4 . \(\dfrac{33}{68}\) = \(\dfrac{33}{17}\)
A = \(\dfrac{33}{17}\) : 7
=> A = \(\dfrac{33}{119}\)
Ta có: \(A=\dfrac{4}{2.5}+\dfrac{4}{5.8}+\dfrac{4}{8.11}+...+\dfrac{4}{65.68}\)
\(=\dfrac{4}{3}\left(\dfrac{3}{2.5}+\dfrac{3}{5.8}+\dfrac{3}{8.11}+...+\dfrac{3}{65.68}\right)\)
\(=\dfrac{4}{3}\left(\dfrac{5-2}{2.5}+\dfrac{8-5}{5.8}+\dfrac{11-8}{8.11}+...+\dfrac{68-65}{65.68}\right)\)
\(=\dfrac{4}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{65}-\dfrac{1}{68}\right)\)
\(=\dfrac{4}{3}\left(\dfrac{1}{2}-\dfrac{1}{68}\right)=\dfrac{4}{3}.\dfrac{33}{68}=\dfrac{11}{17}\)

a: \(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{201}-\dfrac{1}{203}=\dfrac{202}{203}\)
b: \(=-4\left(\dfrac{1}{2\cdot5}+\dfrac{1}{5\cdot8}+...+\dfrac{1}{2015\cdot2018}\right)\)
\(=-\dfrac{4}{3}\cdot\left(\dfrac{3}{2\cdot5}+\dfrac{3}{5\cdot8}+...+\dfrac{3}{2015\cdot2018}\right)\)
\(=\dfrac{-4}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{2015}-\dfrac{1}{2018}\right)\)
\(=\dfrac{-4}{3}\cdot\dfrac{504}{1009}=-\dfrac{672}{1009}\)

Lời giải:
Đặt \(A=1+\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+...+\frac{18}{3^{18}}\)
\(\Rightarrow 3A=3+1+\frac{2}{3}+\frac{3}{3^2}+...+\frac{18}{3^{17}}\)
\(\Rightarrow 3A-A=3+\frac{2-1}{3}+\frac{3-2}{3^2}+\frac{4-3}{3^3}+..+\frac{18-17}{3^{17}}-\frac{18}{3^{18}}\)
\(2A=3+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{17}}-\frac{18}{3^{18}}\)
\(\Rightarrow 6A=9+1+\frac{1}{3}+\frac{1}{3^2}+..+\frac{1}{3^{16}}-\frac{18}{3^{17}}\)
\(\Rightarrow 6A-2A=7-\frac{18}{3^{17}}-\frac{1}{3^{17}}+\frac{18}{3^{18}}\)
\(\Leftrightarrow 4A=7+\frac{18}{3^{18}}-\frac{19}{3^{17}}=7-\frac{39}{3^{18}}\)
\(\Rightarrow A=\frac{1}{4}\left(7-\frac{39}{3^{18}}\right)\)

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)

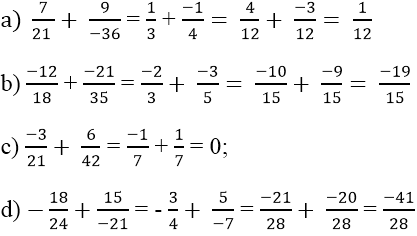
\(A=\dfrac{18}{2.5}+\dfrac{18}{5.8}+...+\dfrac{18}{203.206}\)
\(A=\dfrac{6.3}{2.5}+\dfrac{6.3}{5.8}+...+\dfrac{6.3}{203.206}\)
\(A=6\left(\dfrac{3}{2.5}+\dfrac{3}{5.8}+...+\dfrac{3}{203.206}\right)\)
\(A=6\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{203}-\dfrac{1}{206}\right)\)
\(A=6\left(\dfrac{1}{2}-\dfrac{1}{206}\right)\)
\(A=6.\dfrac{51}{103}\)
\(A=\dfrac{306}{103}\)
18/(2.5) + 18/(5.8) + .... + 18/(203.206)
= 18.[1/(2.5) + 1/(5.8) + .... + 1/(203.206)]
= 18.(1/2 - 1/5 + 1/5 - 1/8 + .... + 1/203 - 1/206)
=18.(1/2 - 1/206)
=18.(51/103)
=918/103