Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x:3\dfrac{1}{15}\) - \(\dfrac{3}{4}\) = 2\(\dfrac{1}{4}\)
\(x\): \(\dfrac{46}{15}\) - \(\dfrac{3}{4}\) = \(\dfrac{9}{4}\)
\(x\) : \(\dfrac{46}{15}\) = \(\dfrac{9}{4}\) + \(\dfrac{3}{4}\)
\(x\) : \(\dfrac{46}{15}\) = \(\dfrac{12}{4}\)
\(x\) : \(\dfrac{46}{15}\) = \(3\)
\(x\) = 3 \(\times\) \(\dfrac{46}{15}\)
\(x\) = \(\dfrac{46}{5}\)
\(x\) \(\times\) 3\(\dfrac{2}{3}\) - 1\(\dfrac{2}{3}\) = 2\(\dfrac{1}{3}\)
\(x\) \(\times\) \(\dfrac{11}{3}\) - \(\dfrac{5}{3}\) = \(\dfrac{7}{3}\)
\(x\) \(\times\) \(\dfrac{11}{3}\) = \(\dfrac{7}{3}\) + \(\dfrac{5}{3}\)
\(x\) \(\times\) \(\dfrac{11}{3}\) = \(\dfrac{12}{3}\)
\(x\times\dfrac{11}{3}\) = 4
\(x\) = 4 : \(\dfrac{11}{3}\)
\(x\) = \(\dfrac{12}{11}\)

`a, 2/3 +3/4 = (8+9)/12=17/12.`
`1 1/3+4/5 = 4/3 + 4/5 = (20+12)/15=32/15`.
`=> x=2.`
`b, 5/6-1/4=(20-6)/24=7/12`.
`2 1/3-2/5= 7/3-2/5 = (35-6)/15=29/15`.
`=> x=1`.

a: \(x\cdot\dfrac{3}{4}+x=\dfrac{7}{8}\)
\(\Leftrightarrow x\cdot\dfrac{7}{4}=\dfrac{7}{8}\)
\(\Leftrightarrow x=\dfrac{1}{2}\)

a) \(\dfrac{2}{3}+\dfrac{3}{4}< x< 1\dfrac{1}{3}+\dfrac{4}{5}\)
\(\dfrac{2\times4}{3\times4}+\dfrac{3\times3}{4\times3}< x< \dfrac{\left(1\times3+1\right)\times5}{3\times5}+\dfrac{4\times3}{5\times3}\)
\(\dfrac{8}{12}+\dfrac{9}{12}< x< \dfrac{20}{15}+\dfrac{12}{15}\\ \dfrac{17}{12}< x< \dfrac{32}{15}\)
Ước tính: \(\dfrac{17}{12}=1,4\) và \(\dfrac{32}{15}=2,1\). Vậy số tự nhiên x = 2 sẽ thõa mãn 1,4 < x < 2,1
b)
\(\dfrac{5}{6}-\dfrac{1}{4}< x< 2\dfrac{1}{3}-\dfrac{2}{5}\\ \dfrac{5\times4}{6\times4}-\dfrac{1\times6}{4\times6}< x< \dfrac{\left(2\times3+1\right)\times5}{3\times5}-\dfrac{2\times3}{5\times3}\\ \dfrac{20}{24}-\dfrac{6}{24}< x< \dfrac{35}{15}-\dfrac{6}{15}\\ \dfrac{14}{24}< x< \dfrac{29}{15}\)
Ước tính \(\dfrac{14}{24}=0,5\) và \(\dfrac{29}{15}=1,9\)
Vậy với x là số tự nhiên x = 1 sẽ thõa mãn 0,5 < x < 1,9

29\(\dfrac{1}{2}\)\(\times\)\(\dfrac{2}{3}\) + 39\(\dfrac{1}{3}\)\(\times\)\(\dfrac{3}{4}\) + \(\dfrac{5}{6}\)
= \(\dfrac{59}{2}\) \(\times\) \(\dfrac{2}{3}\) + \(\dfrac{118}{3}\) \(\times\) \(\dfrac{3}{4}\) + \(\dfrac{5}{6}\)
= \(\dfrac{59}{3}\) + \(\dfrac{59}{2}\) + \(\dfrac{5}{6}\)
= \(\dfrac{295}{6}\) + \(\dfrac{5}{6}\)
= 50

= 59/2 x 2/3+ 118/3 x 3/4 + 5/6
= 59/3+ 59/2+ 5/6
= 118/6+ 177/6+ 5/6
= 50
= 59/2 x 2/3+ 118/3 x 3/4 + 5/6
= 59/3+ 59/2+ 5/6
= 118/6+ 177/6+ 5/6
= 50

a)
\(=\dfrac{13}{5}+\dfrac{7}{5}\cdot\dfrac{7}{2}\)
\(=\dfrac{13}{5}+\dfrac{49}{10}\\ =\dfrac{26}{10}+\dfrac{49}{10}\\ =\dfrac{15}{2}\)
b)
\(=\dfrac{52}{4}-\dfrac{11}{3}:\dfrac{7}{6}\)
\(=\dfrac{52}{4}-\dfrac{22}{7}\\ =\dfrac{69}{7}\)
a) $2\dfrac35 + 1\dfrac25 . 3\dfrac12$
$= \dfrac{13}5 + \dfrac75.\dfrac72$
$= \dfrac{26}{10} + \dfrac{49}{10}$
$=\dfrac{15}2$.
b) $4\dfrac34 - 3\dfrac23 : 1\dfrac16$
$= \dfrac{19}4 - \dfrac{11}3 : \dfrac76$
$= \dfrac{19}4 - \dfrac{11}3 . \dfrac67$
$= \dfrac{19}4 - \dfrac{22}7$
$= \dfrac{45}{28}$.

\(\Rightarrow x+\dfrac{1}{6}=\dfrac{3}{4}\\ \Rightarrow x=\dfrac{7}{12}\)

\(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}\\ =1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}\\ =1-\dfrac{1}{11}=\dfrac{10}{11}\)
\(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+\dfrac{2}{9\cdot11}\\ =1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}\\ =1-\dfrac{1}{11}\\ =\dfrac{10}{11}\)
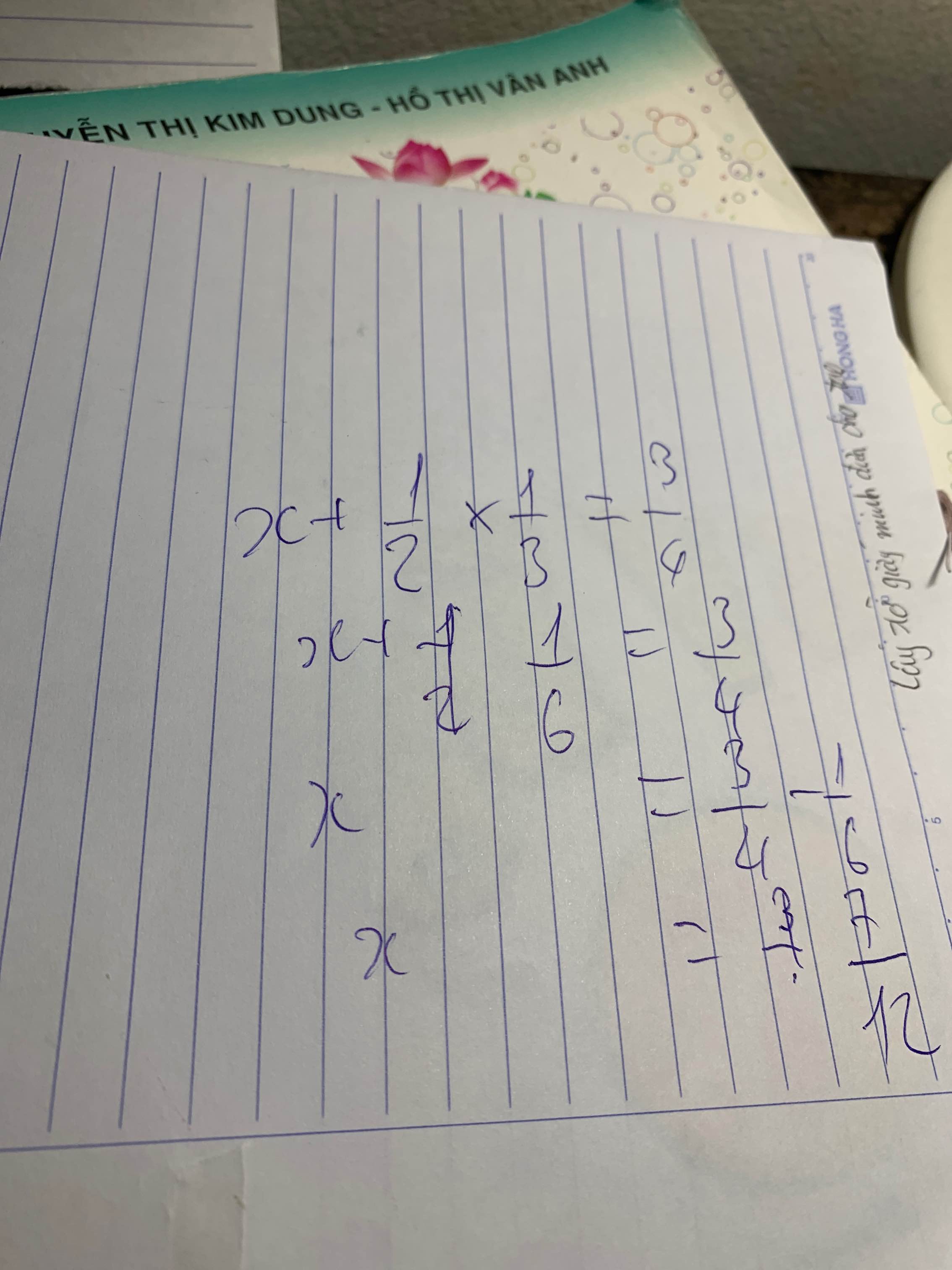

\(\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+\dfrac{1}{1+2+3+4}+\dfrac{1}{1+2+3+...+100}\)
=\(\dfrac{1}{\left(1+2\right)\cdot2:2}+\dfrac{1}{\left(1+3\right)\cdot3:2}+\dfrac{1}{\left(1+4\right)\cdot4:2}+...+\dfrac{1}{\left(1+100\right)\cdot100:2}\)
=\(\dfrac{2}{2\cdot3}+\dfrac{2}{3\cdot4}+\dfrac{2}{4\cdot5}+...+\dfrac{2}{100\cdot101}\)
=\(2\cdot\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{100\cdot101}\right)\)
=\(2\cdot\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{100}-\dfrac{1}{101}\right)\)
=\(2\cdot\left(\dfrac{1}{2}-\dfrac{1}{101}\right)\)
=\(2\cdot\dfrac{99}{202}\)
=\(\dfrac{198}{202}\)