Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(l=\dfrac{1}{1.4}+\dfrac{1}{4.7}+\dfrac{1}{7.10}+....+\dfrac{1}{97.100}\)
\(=\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{3}\left(1-\dfrac{1}{100}\right)=\dfrac{1}{3}-\dfrac{1}{300}< \dfrac{1}{3}\left(đpcm\right)\)

\(\dfrac{1}{3}\)x(\(\dfrac{3}{1+4}\)+\(\dfrac{3}{4+7}\)+........+\(\dfrac{3}{101+103}\))
\(\dfrac{1}{3}\)x(\(\dfrac{1}{1}\)-\(\dfrac{1}{4}\)+\(\dfrac{1}{4}\)-\(\dfrac{1}{7}\)+.........+\(\dfrac{ }{ }\)\(\dfrac{1}{101}\)-\(\dfrac{1}{103}\))
\(\dfrac{1}{3}\)x(\(\dfrac{1}{1}\)-\(\dfrac{1}{103}\))
\(\dfrac{1}{3}\)x\(\dfrac{102}{103}\)
\(\dfrac{34}{103}\)
\(\dfrac{1}{1.4}+\dfrac{1}{4.7}+\dfrac{1}{7.10}+...+\dfrac{1}{100.103}\)
\(=\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{100}-\dfrac{1}{103}\)
\(=\dfrac{1}{1}-\dfrac{1}{103}\)
\(=\dfrac{102}{103}\)

a: \(A=6\left(x+\dfrac{1}{3}\right)^2-7>=-7>-8\forall x\)
\(B=-8-\left(3.75-x\right)^2\le-8\)
Do đó: A>B
b: \(A=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{16}=\dfrac{15}{16}\)
\(B=\left(\dfrac{1}{2}\right)^4=\dfrac{1}{16}\)
Do đó: A>B

\(a,A=\dfrac{101}{100}+\dfrac{102}{100}+\dfrac{103}{100}+...+\dfrac{199}{100}\)
\(A=\dfrac{101+102+103+...+109}{100}\)
Xét tử số : \(101+102+103+...+199\)
Có : \(\left(199-101\right):1+1=99\) (số hạng)
\(\Rightarrow\) Tử số bằng \(:\left(199+101\right).99:2=14850\)
\(\Rightarrow A=\dfrac{14850}{100}=\dfrac{297}{2}\)
\(b,B=\dfrac{10002}{10000}+\dfrac{10004}{10000}+\dfrac{10006}{10000}+...+\dfrac{12014}{10000}\)
\(B=\dfrac{10002+10004+10006+...+12014}{10000}\)
\(B=\dfrac{10002+10004+10006+...+12014}{10000}\)
Xét tử số : \(10002+10004+10006+...+12014\)
Có : \(\left(12014-10002\right):2+1=1007\) (số hạng)
\(\Rightarrow\) Tử số bằng : \(\left(12014+10002\right).1007:2=11085056\)
\(\Rightarrow B=\dfrac{11085056}{10000}\)
Bạn tự làm câu C nha
\(D=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{2014.2015}\)
\(\Rightarrow D=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{2014}-\dfrac{1}{2015}\)
\(\Rightarrow D=\dfrac{1}{5}-\dfrac{1}{2015}=\dfrac{402}{2015}\)
\(E=\dfrac{1}{1.4}+\dfrac{1}{4.7}+\dfrac{1}{7.10}+...+\dfrac{1}{2014.2017}\)
\(\Rightarrow3E=\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{2014.2017}\)
\(\Rightarrow3E=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{2014}-\dfrac{1}{2017}\)
\(\Rightarrow3E=1-\dfrac{1}{2017}=\dfrac{2016}{2017}\)
\(\Rightarrow E=\dfrac{2016}{2017}:3=\dfrac{672}{2017}\)
D = \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\) + \(\dfrac{1}{7.8}\) +...+ \(\dfrac{1}{2014.2015}\)
D = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)+...+ \(\dfrac{1}{2014}-\dfrac{1}{2015}\)
D = \(\left(\dfrac{1}{5}-\dfrac{1}{2015}\right)\)
D = \(\dfrac{403}{2015}-\dfrac{1}{2015}\)
D = \(\dfrac{402}{2015}\)

a) \(\left(x+\dfrac{1}{2}\right)+\left(x+\dfrac{1}{6}\right)+\left(x+\dfrac{1}{12}\right)+....+\left(x+\dfrac{1}{9900}\right)\)
\(\Leftrightarrow\left(x+x+x+...+x\right)+\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{9900}\right)=1\)
\(\Leftrightarrow50x+\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\right)=1\)
\(\Leftrightarrow50x+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)=1\)
\(\Leftrightarrow50x+\left(1-\dfrac{1}{100}\right)=1\)
\(\Leftrightarrow50x+\dfrac{99}{100}=1\)
\(\Leftrightarrow50x=\dfrac{1}{100}\Rightarrow x=\dfrac{1}{5000}\)
b) \(A=\dfrac{3^2}{1.4}+\dfrac{3^2}{4.7}+\dfrac{3^2}{7.10}+...+\dfrac{3^2}{202.205}\)
\(A=\dfrac{3^2}{3}\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{202}-\dfrac{1}{205}\right)\)
\(A=\dfrac{9}{3}\cdot\left(1-\dfrac{1}{205}\right)\)
\(A=\dfrac{9}{3}\cdot\dfrac{204}{205}=\dfrac{615}{205}\)
a) \(\left(x+\dfrac{1}{2}\right)+\left(x+\dfrac{1}{6}\right)+\left(x+\dfrac{1}{12}\right)+....+\left(x+\dfrac{1}{9900}\right)=1\)
\(\Leftrightarrow\left(x+x+x+...+x\right)+\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{9900}\right)=1\)
\(\Leftrightarrow\left(x+x+x+...+x\right)+\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\right)=1\)
Có tất cả : (99 - 1) : 1 + 1 = 99 (số x)
\(\Rightarrow99x+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)=1\)
\(\Rightarrow99x+\left(1-\dfrac{1}{100}\right)=1\)
\(\Rightarrow99x+\dfrac{99}{100}=1\Rightarrow99x=1-\dfrac{99}{100}\)
\(\Rightarrow99x=\dfrac{1}{100}\Rightarrow x=\dfrac{1}{100.99}=\dfrac{1}{9900}\)
b) \(A=\dfrac{3^2}{1.4}+\dfrac{3^2}{4.7}+\dfrac{3^2}{7.10}+....+\dfrac{3^2}{202.205}\)
\(A=\dfrac{3^2}{3}\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{202}-\dfrac{1}{205}\right)\)
\(A=\dfrac{9}{3}\cdot\left(1-\dfrac{1}{205}\right)\)
\(A=3\cdot\dfrac{204}{205}=\dfrac{615}{205}\)

\(\Leftrightarrow\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{x\left(x+3\right)}=\dfrac{375}{376}\)
\(\Leftrightarrow1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{x}-\dfrac{1}{x+3}=\dfrac{375}{376}\)
\(\Leftrightarrow1-\dfrac{1}{x+3}=\dfrac{375}{376}\)
\(\Leftrightarrow\dfrac{1}{x+3}=1-\dfrac{375}{376}=\dfrac{1}{376}\)
\(\Rightarrow x+3=376\)
\(\Rightarrow x=373\)

\(\Leftrightarrow\dfrac{1}{3}\left(\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-...+\dfrac{1}{97}-\dfrac{1}{100}\right)=\dfrac{0,33x}{2009}\)
\(\Leftrightarrow\dfrac{1}{3}\cdot\dfrac{99}{100}=\dfrac{0,33x}{2009}\)
\(\Leftrightarrow\dfrac{33}{100}=\dfrac{0,33x}{2009}\) <=> x = (tự tính )
⇔13(11−14+14−...+197−1100)=0,33x2009⇔13(11−14+14−...+197−1100)=0,33x2009
⇔13⋅99100=0,33x2009⇔13⋅99100=0,33x2009
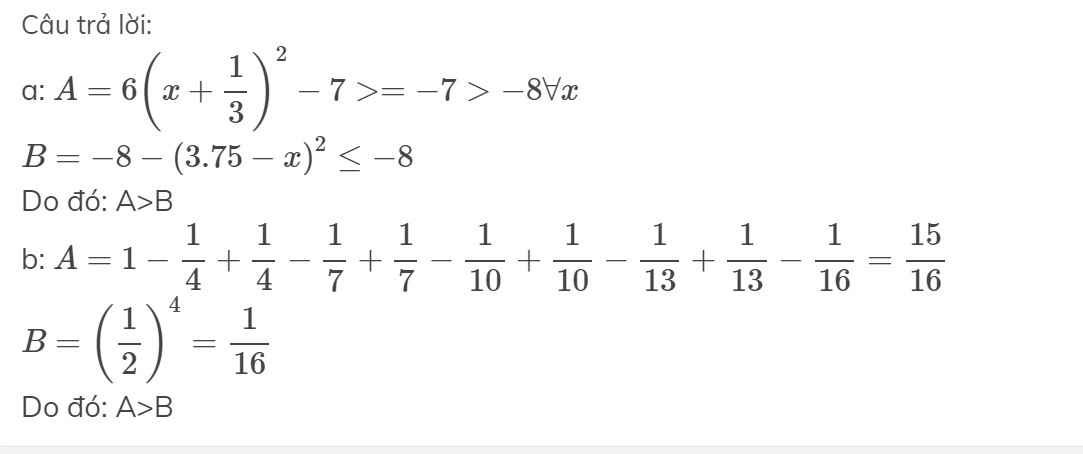
A = \(-\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{2017}-\dfrac{1}{2020}\right)=-1+\dfrac{1}{2020}=\dfrac{-2019}{2020}\)
dấu trừ tại sao lại thành cộng vậy bạn?