K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5
ST
3
22 tháng 4 2016
Công thức tính số tam giác nếu đề bài cho n điểm không thẳng hàng, cứ 3 điểm ko thẳng hàng= 1 tam giác. Hỏi có bao nhiêu tam giác:
Mình nghĩ là: \(\frac{n\left(n-1\right)}{2}\)
7 tháng 12 2021
Hình lục giác đều được ghép bởi 6 tam giác đều
\(\Rightarrow\) Hình lục giác đều có cạnh là 3 cm nhé!
21 tháng 9
Khi nhìn vào hình, ta có nhận xét : khi hình tam giác đều có cạnh bằng 3 cm thì cạnh của lục giác đều cũng có 3cm vì cạnh của hình lục giác đều chính là cạnh của hình tam giác đều.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
20 tháng 9 2023
Cứ 1 điểm sẽ tạo với 10 - 1 điểm còn lại: 10 - 1 (đoạn thẳng)
a, Với 10 điểm sẽ tạo được: (10 - 1)\(\times\)10 (đoạn thẳng)
Theo cách tính trên mỗi đoạn thẳng được tính hai lần. Vậy thực tế số đoạn thẳng là:
(10 - 1) \(\times\) 10: 2 = 45 (đoạn thẳng)
b, Cứ 3 điểm không thẳng hàng sẽ tạo thành 1 tam giác, mổi điểm là 1 đỉnh của tam giác. Với 10 điểm trong đó không có ba điểm nào thẳng hàng ta có:
10 cách chọn đỉnh thứ nhất
9 cách chọn đỉnh thứ hai
8 cách chọn đỉnh thứ ba
Số tam giác được tạo là: 10 \(\times\) 9 \(\times\) 8 = 720 (tam giác)
Theo cách tính trên mỗi tam giác sẽ được tính sáu lần.
Tất cả số tam giác được tạo thành là: 720 : 6 = 120 (tam giác)
Kết luận:...
NV
Nguyễn Việt Dũng
CTVVIP
10 tháng 11 2023
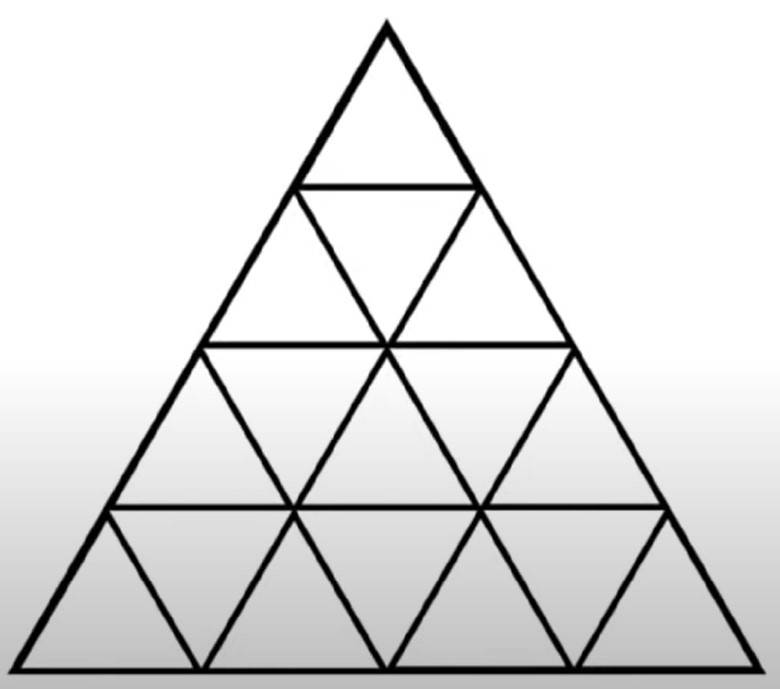
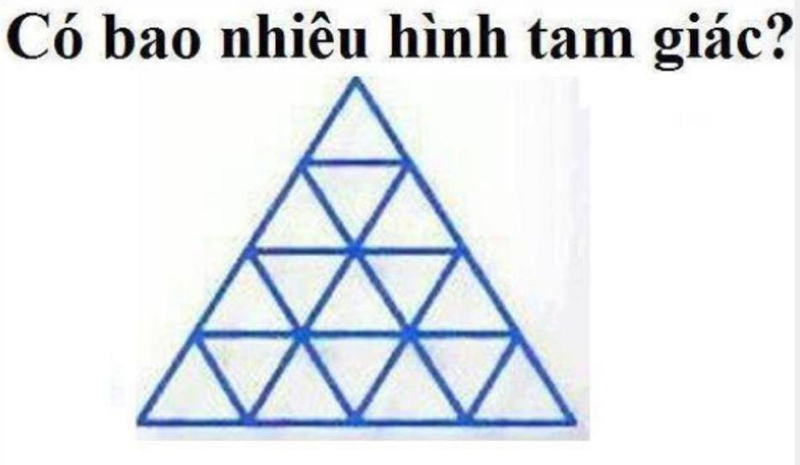
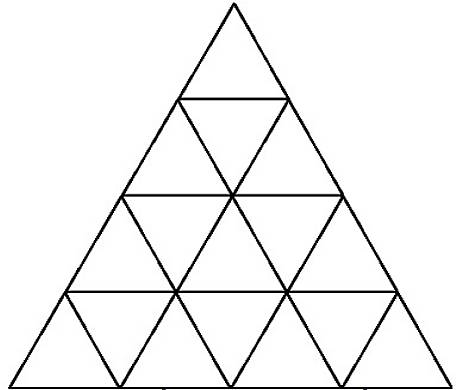
Ta có số lượng tam giác trên mỗi tầng tăng lên theo quy luật số hình tam giác bằng bình phương của số tầng:
Tầng 1: 1^2 = 1 tam giác
Tầng 2: 2^2 = 4 tam giác
Tầng 3: 3^2 = 9 tam giác
Tầng 4: 4^2 = 16 tam giác
Vậy tổng số tam giác cho một tháp 4 tầng sẽ là tổng của các số trên:
1 + 4 + 9 + 16 = 30 tam giác
Như vậy, một tháp tam giác với độ cao là 4 tầng sẽ có tổng cộng 30 hình tam giác.
HÌNH ĐÂU
hình tải lên rồi nhưng ko được