
Gọi thời gian đội I làm một mình xong công việc là x (ngày) (x > 4)
Nếu họ làm riêng thì đội I hoàn thành công việc nhanh hơn đội II là 6 ngày
⇒ thời gian một mình đội II làm xong công việc là x + 6 (ngày).
Mỗi ngày, đội I làm được: 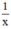 (công việc); đội II làm được
(công việc); đội II làm được 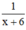 (công việc).
(công việc).
⇒ Một ngày cả hai đội cùng làm được: 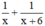 (công việc).
(công việc).
Cả hai đội cùng làm thì trong 4 ngày xong việc nên một ngày cả hai đội cùng làm được 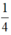 công việc.
công việc.
Vậy ta có phương trình:
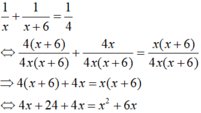
⇔ 8 x + 24 = x 2 + 6 x ⇔ x 2 – 2 x – 24 = 0
Có a = 1; b = -2; c = -24 ⇒ Δ ’ = ( - 1 ) 2 – 1 . ( - 24 ) = 25 > 0
Phương trình có hai nghiệm
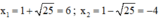
Trong hai nghiệm chỉ có nghiệm x = 6 thỏa mãn điều kiện.
Vậy:
Một mình đội I làm trong 6 ngày thì xong việc.
Một mình đội II làm trong 12 ngày thì xong việc.
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.

Gọi thời gian đội I làm một mình xong công việc là x (ngày) (x > 4)
Nếu họ làm riêng thì đội I hoàn thành công việc nhanh hơn đội II là 6 ngày
⇒ thời gian một mình đội II làm xong công việc là x + 6 (ngày).
Mỗi ngày, đội I làm được: 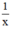 (công việc); đội II làm được
(công việc); đội II làm được 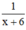 (công việc).
(công việc).
⇒ Một ngày cả hai đội cùng làm được: 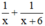 (công việc).
(công việc).
Cả hai đội cùng làm thì trong 4 ngày xong việc nên ta có phương trình:
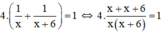
⇔ 4.(2x + 6) = x(x + 6)
⇔ 8x + 24 = x2 + 6x
⇔ x2 – 2x – 24 = 0
Có a = 1; b = -2; c = -24 ⇒ Δ’ = (-1)2 – 1.(-24) = 25 > 0
Phương trình có hai nghiệm
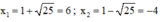
Trong hai nghiệm chỉ có nghiệm x = 6 thỏa mãn điều kiện.
Vậy:
Một mình đội I làm trong 6 ngày thì xong việc.
Một mình đội II làm trong 12 ngày thì xong việc.

Gọi thời gian làm riêng để hoàn thành công việc của đội 1 là x>0 (ngày), đội 2 là y>0 (ngày)
Trong 1 ngày hai đội lần lượt làm được \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần công việc
Do 2 đội làm chung thì hoàn thành sau 12 ngày nên: \(12\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\)
Do đội 1 hoàn thành chậm hơn đội 2 là 10 ngày nên: \(x=y+10\)
Ta có hệ pt:
\(\left\{{}\begin{matrix}12\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\\x=y+10\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}12\left(\dfrac{1}{y+10}+\dfrac{1}{y}\right)=1\\x=y+10\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}12\left(2y+10\right)=y\left(y+10\right)\\x=y+10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y^2-14y-120=0\\x=y+10\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y=20\\x=30\end{matrix}\right.\)

Gọi thời gian làm 1 mình xong việc của đội 1 là x ngày và của đội 2 là y ngày (với x>10;y>0)
Trong 1 ngày đội 1 làm được \(\dfrac{1}{x}\) phần công việc và đội 2 làm được \(\dfrac{1}{y}\) phần công việc
Do làm riêng đội 1 làm chậm hơn đội 2 là 10 ngày nên ta có:
\(x-y=10\) (1)
Hai đội làm chung trong 1 ngày được \(\dfrac{1}{x}+\dfrac{1}{y}\) phần công việc
Do 2 đội làm chung thì hoàn thành trong 12 ngày nên ta có:
\(12\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}x-y=10\\12\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y=x-10\\12\left(x+y\right)=xy\end{matrix}\right.\)
Thế pt trên xuống pt dưới:
\(12\left(x+x-10\right)=x\left(x-10\right)\)
\(\Leftrightarrow x^2-34x+120=0\Rightarrow\left[{}\begin{matrix}x=30\\x=4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow y=x-10=20\)
Vậy đội 1 làm 1 mình xong trong 30 ngày và đội 2 xong trong 20 ngày
Gọi thời gian làm riêng hoàn thành công việc của đội một là x(ngày)
(Điều kiện: x>10)
Thời gian làm riêng hoàn thành công việc của đội 2 là x-10(ngày)
Trong 1 ngày, đội 1 làm được \(\dfrac{1}{x}\left(côngviệc\right)\)
Trong 1 ngày, đội 2 làm được \(\dfrac{1}{x-10}\left(côngviệc\right)\)
Trong 1 ngày, hai đội làm được \(\dfrac{1}{12}\left(côngviệc\right)\)
Do đó, ta có phương trình:
\(\dfrac{1}{x}+\dfrac{1}{x-10}=\dfrac{1}{12}\)
=>\(\dfrac{x-10+x}{x\left(x-10\right)}=\dfrac{1}{12}\)
=>\(x\left(x-10\right)=12\left(2x-10\right)\)
=>\(x^2-10x=24x-120\)
=>\(x^2-34x+120=0\)
=>(x-30)(x-4)=0
=>\(\left[{}\begin{matrix}x-30=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=30\left(nhận\right)\\x=4\left(loại\right)\end{matrix}\right.\)
Vậy: Thời gian làm riêng hoàn thành công việc của đội 1 là 30 ngày
Thời gian làm riêng hoàn thành công việc của đội 2 là 30-10=20 ngày

Bài giải:
Gọi thời gian đội I làm một mình xong việc là x (ngày), x > 0.
Vì đội II hoàn thành công việc lâu hơn đội I là 6 ngày nên thời gian một mình đội II làm xong việc là x + 6 (ngày).
Mỗi ngày đội I làm được 1/x (công việc).
Mỗi ngày đội II làm được 1/x+6 (công việc)
Ta có phương trình: 1/x + 1/x+6 = 1/4
Giải phương trình: x(x + 6) = 4x + 4x + 24 hay x2– 2x - 24 = 0, ∆' = 1 + 24 = 25 = 52
x1 = 1 + 5 = 6, x2 = 1 - 5 = -4
Vì x > 0 nên x2 = -4 không thỏa mãn điều kiện của ẩn.
Trả lời: Một mình đội I làm trong 6 ngày thì xong việc.

Gọi thời gian đội I làm một mình xong việc là x (ngày), x > 0.
Vì đội II hoàn thành công việc lâu hơn đội I là 6 ngày nên thời gian một mình đội II làm xong việc là x + 6 (ngày).
Mỗi ngày đội I làm được (công việc).
Mỗi ngày đội II làm được (công việc)
Ta có phương trình: +
=
Giải phương trình: x(x + 6) = 4x + 4x + 24 hay x2– 2x - 24 = 0, ∆' = 1 + 24 = 25 = 52
x1 = 1 + 5 = 6, x2 = 1 - 5 = -4
Vì x > 0 nên x2 = -4 không thỏa mãn điều kiện của ẩn.
Trả lời: Một mình đội I làm trong 6 ngày thì xong việc.
Một mình đội II làm trong 12 ngày thì xong việc.
Gọi thời gian làm việc của hai đội lần lượt là aa (ngày), bb (ngày) (a,b>0 và a,b∈N)(a,b>0 và a,b∈N)
Khi đó trong 1 ngày đội thứ nhất làm được 1a1a (công việc),
trong 1 ngày đội thứ hai làm được 1b1b (công việc)
Vì hai đội cùng làm thì trong 6 ngày là xong việc nên
6.1a+6.1b=16.1a+6.1b=1 (1)
Ta lại có: khi làm riêng thì đội thứ nhất hoàn thành công việc chậm hơn đội thứ hai là 9 ngày
⇒a=b+9⇒a=b+9 (2)
Thay (2) và (1) ta có
6.1b+9+6.1b=16.1b+9+6.1b=1
⇔6(b+b+9)=(b+9
Đúng(0)
Goi thoi gian lm rieng cua doi 1 la : x ( ngay )
dkxd : x > 6
Thoi gian " " doi 2 la : x +9
1 ngay doi 1 lm dc so cv la :1/x (cv)
1 ngay doi 2 lm dc so cv la :1/x+9 ( cv)
Theo bai ra thi 2 doi cung lm thi trong 6 ngay xong viec ,nen ta co pt:
1/x + 1/x+9 =1/6 ≫ 6(x+9) + 6x =x(x+9) ≫ x' - 3x - 54 =0
Ta co : ▲= b' - 4ac
▲=15
Do ▲>0 nen ta co pt:
x1 =9 (tm) ; x2= -6 (loai)
Doi thu 1 lm rieng thi sau 18 ngay thi xong , doi thu 2 lm rieng thi can so ngay la : 18 - 9= 9 (ngay)
Vay neu lm rieng doi 1 can 18 ngay ,doi 2 can 9 ngay