Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

diện tích xung quanh căn nhà là:
(12+4)x2x3,5=112(m2)
diện tích quét sơn (không tính cửa sổ) là:
112-10,2=101,8(m2)
diện tích toàn bộ cần quét sơn là:
101,8+(3,5+2,5)x2x3,5=143,8(m2)
số tiền cần trả là:
143,8x20000=2876000(đồng)
đáp số: 2876000 đồng

Gọi t1 (giờ) là thời gian người thứ nhất sơn xong bức tường,
t2 (giờ) là thời gian người thứ hai sơn xong bức tường.
(Điều kiện: t1 > 0; t2 > 0)
+ Trong một giờ:
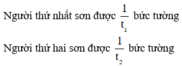
+ Người thứ nhất làm trong 7 giờ và người thứ hai làm trong 4 giờ thì họ sơn được 5/9 bức tường nên ta có: 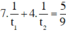
+ Sau đó họ cùng làm việc với nhau trong 4 giờ nữa, nghĩa là người thứ nhất làm trong 7 + 4 = 11 giờ và người thứ hai làm trong 4 + 4 = 8 giờ.
Khi đó họ còn 1/18 bức tường chưa sơn nghĩa là họ đã sơn được 17/18 bức tường.
Ta có phương trình 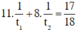
Ta có hệ phương trình 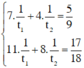
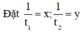 , khi đó hệ phương trình trở thành
, khi đó hệ phương trình trở thành 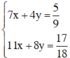
Giải hệ phương trình trên ta được 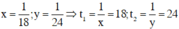
Vậy nếu mỗi người làm riêng thì người thứ nhất sơn xong bức tường trong 18 giờ, người thứ hai sơn xong bức tường trong 24 giờ.

Bạn vẽ cho mình cái hình minh họa đi. Chứ nói vầy mình không hiểu theo b thì như thế nào gọi là rõ nhất nữa
mình đâu biết vẽ hình đâu....vẽ hình ra thì chắc mình cũng biết làm![]()
![]()

Gọi x (giờ), y(giờ) là thời gian để công nhân thứ nhất, thứ hai làm riêng để sơn xong bức tường.
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{7}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{4}{y}=1-\dfrac{5}{9}-\dfrac{1}{18}=\dfrac{7}{18}\end{matrix}\right.\)
Giải hệ phương trình trên ta được: \(\dfrac{1}{x}=\dfrac{1}{18};\dfrac{1}{y}=\dfrac{1}{24}\)
Suy ra x = 18, y = 24.
Vậy mỗi người làm riêng, theo thứ tự, thời gian sơn xong bức tường là 18 giờ và 24 giờ.

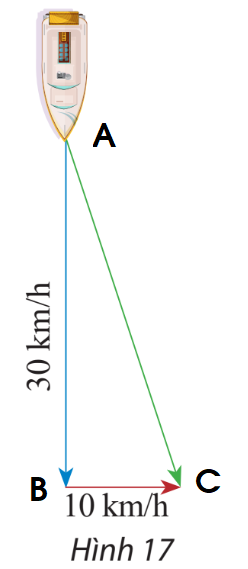
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.
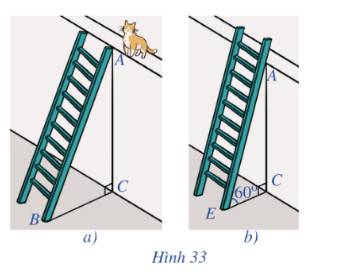


Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.