Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

F là một hàm số theo biến C vì với mỗi giá trị của C chỉ cho ta duy nhất một giá trị của F.

nhiệt độ f của thành phố hồ chí minh là
\(F=\frac{9}{5}C+32\)\(=\frac{9}{5}.35+32=63+32=95\)(độ F)

Thay C=10 vào \(C = \frac{5}{9}\left( {F - 32} \right)\), có:
\(\frac{5}{9}\left( {F - 32} \right) = 10\)
F − 32 = 18
F = 50

Thân nhiệt của người đó theo độ C là trog khoảng: 206,6 độ C đến 211,1 độ

À có ai không hiểu gì thì hỏi nha! Còn ai muốn click "đúng" cho anh thì cho anh cảm ơn!
Cách khác cho bài đầu:
Ta có: \(a+b=6-c\le5\)
\(a^2+b^2+c^2=a.a+b.b+c.c\)
\(=\left(a-b\right)a+\left(b-c\right)\left(a+b\right)+c\left(a+b+c\right)\)
\(\le\left(a-b\right).3+5\left(b-c\right)+6c\)
\(=3a+2b+c=\left(a+b+c\right)+a+\left(a+b\right)\)
\(\le6+3+5=14\)
Đẳng thức xảy ra khi \(\left(a;b;c\right)=\left(3;2;1\right)\) và các hoán vị của nó.
Cách này dường như ez hơn ấy nhỉ? Mà đúng không ta:3

a) Ta có:
\(f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};\)
\(f\left( { - 5} \right) = \dfrac{5}{{4.\left( { - 5} \right)}} = \dfrac{5}{{ - 20}} = \dfrac{{ - 1}}{4};\)
\(f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}\)
b) Ta có:
\(f\left( { - 3} \right) = \dfrac{5}{{4.\left( { - 3} \right)}} = \dfrac{5}{{ - 12}} = \dfrac{{ - 5}}{{12}};\)
\(f\left( { - 2} \right) = \dfrac{5}{{4.\left( { - 2} \right)}} = \dfrac{5}{{ - 8}} = \dfrac{{ - 5}}{8};\)
\(f\left( { - 1} \right) = \dfrac{5}{{4.\left( { - 1} \right)}} = \dfrac{5}{{ - 4}} = \dfrac{{ - 5}}{4};\)
\(f\left( { - \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { - \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ - 4}}{2}}} = \dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\);
\(f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5\);
\(f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}\);
\(f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}\)
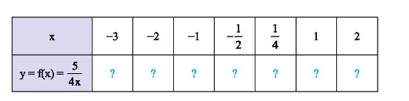
Ta có bảng sau:
\(x\) | –3 | –2 | –1 | \( - \dfrac{1}{2}\) | \(\dfrac{1}{4}\) | 1 | 2 |
\(y = f\left( x \right) = \dfrac{5}{{4x}}\) | \(\dfrac{{ - 5}}{{12}}\) | \(\dfrac{{ - 5}}{8}\) | \(\dfrac{{ - 5}}{4}\) | \(\dfrac{{ - 5}}{2}\) | 5 | \(\dfrac{5}{4}\) | \(\dfrac{5}{8}\) |
a) Ta có: \(C = \dfrac{5}{9}.\left( {F - 32} \right) = \dfrac{5}{9}F - \dfrac{5}{9}.32 = \dfrac{5}{9}F - \dfrac{{160}}{9}\)
Vì \(C = \dfrac{5}{9}F - \dfrac{{160}}{9}\) có dạng\(C = aF - b\) với \(a = \dfrac{5}{9}\) và \(b = - \dfrac{{160}}{9}\) nên \(C\) là hàm số bậc nhất của biến số \(F\).
b)
- Với \(F = 32 \Rightarrow C = \dfrac{5}{9}.32 - \dfrac{{160}}{9} = \dfrac{{160}}{9} - \dfrac{{160}}{9} = 0\)
Vậy vớ \(F = 32\) thì \(C = 0\).
- Với \(C = 100 \Rightarrow 100 = \dfrac{5}{9}F - \dfrac{{160}}{9}\)
\( \Leftrightarrow \dfrac{5}{9}F = 100 - \dfrac{{160}}{9}\)
\( \Leftrightarrow \dfrac{5}{9}F = \dfrac{{740}}{9}\)
\( \Leftrightarrow F = \dfrac{{740}}{9}:\dfrac{5}{9}\)
\( \Leftrightarrow F = 149\)
Vậy khi \(C = 100\) thì \(F = 149\).