Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: NM//AB
=> \(\dfrac{NM}{AB}=\dfrac{CN}{AC}< =>AB=1,5\cdot\dfrac{20}{1,25}=24\left(m\right)\)
Vậy tòa nhà đó cao 24m

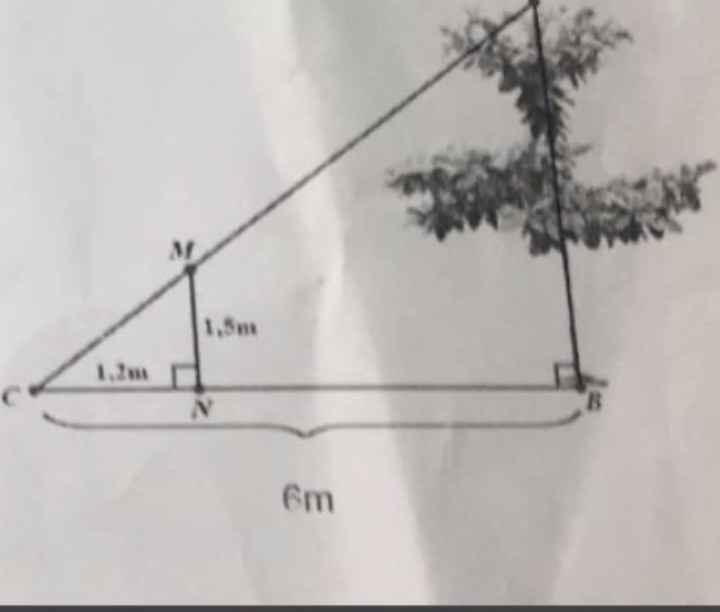
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)

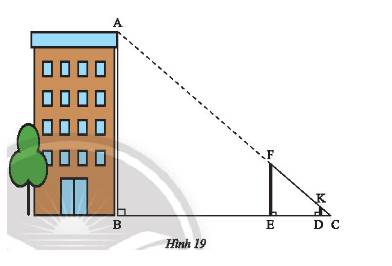
Vì \(\left\{ \begin{array}{l}KD \bot BC\\AB \bot BC\end{array} \right. \Rightarrow KD//AB\).
Xét tam giác \(CAB\) có \(KD//AB \Rightarrow \frac{{KD}}{{AB}} = \frac{{DC}}{{BC}}\) (hệ quả của định lí Thales).
\( \Rightarrow \frac{1}{{AB}} = \frac{{1,2}}{{24}} \Rightarrow AB = \frac{{24.1}}{{1,2}} = 20m\)
Vậy chiều cao \(AB\) của tòa nhà là 20m.

Xét ΔCAB có FE//AB
nên FE/AB=CF/CA
=>6/AB=4/10=2/5
=>AB=15(m)

a: Xét ΔABC có DE//BC
nên AN/AB=AM/AC
=>1,5/AB=2,4/5,3
=>\(AB\simeq3,3125\left(m\right)\)
b: 
Xét ΔABC có DE//BC
nên DE/BC=AE/AC=(AC-CE)/AC
=>36-x=1,6*36/24=2.4
=>x=33,6(m)
a) Xét tam giác \(ABC\) có \(MN//BC\) nên theo định lí Thales ta có:
\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} \Leftrightarrow \frac{{1,5}}{{AB}} = \frac{{2,4}}{{2,4 + 2,9}} \Rightarrow AB = \frac{{1,5.\left( {2,4 + 2,9} \right)}}{{2,4}} = 3,3125\)
Vậy chiều cao \(AB\)của cái cây là 3,3125m.
b) Đặt tên các điểm như hình vẽ

Xét tam giác \(ABC\) có \(DE//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AC - CE}}{{AC}} \Leftrightarrow \frac{{1,6}}{{24}} = \frac{{36 - x}}{{36}}\)
\( \Rightarrow 36 - x = \frac{{1,6.36}}{{24}} \Leftrightarrow x = 36 - \frac{{1,6.36}}{{24}} = 33,6\)
Vậy người đó có thể đứng xa tòa nhà nhất là 33,6m.


Ta có :
\(\dfrac{NM}{AB}\) và \(\dfrac{CN}{CA}\) .
Vì \(\dfrac{NM}{AB}\) = \(\dfrac{CN}{CA}\) \(\Leftrightarrow\) AB = 1,5 . \(\dfrac{20}{1,25}\) = 24 ( m ) .
Vậy chiều cao AB của tòa nhà đó là 24 m .