Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D O M
a) BC vuông góc với AO là theo tính chất hai tiếp tuyến đi qua 1 điểm A
b) Xét hai tam giác DCO và DBA có góc D chung và góc C = góc B = 90 độ (tính chất tiếp tuyến)
=> tam giác DCO đồng dạng với tam giác DBA
=> DC/DB = DO/DA
=> DC.DA = DO.DB (đpcm)
c) Vì OM vuông góc với DB => OM // BA (cùng vuông góc với DB)
Ta có AM/DM + 1 = (AM + DM)/DM = DA/DM
Theo Viet ta có: DA/DM = AB/MO
=> AM/DM + 1 = AB/OM
=> AB/OM - AM/DM = 1 (*)
Ta lại có tam giác MOA cân (vì góc MOA = góc BAO do so le trong, góc MAO = góc BAO do tính chất hai tiếp tuyến cùng 1 điểm)
=> OM = AM
(*) trở thành: AB/AM - AM/DM = 1 (đpcm)

Tớ không vẽ hình được bạn tự vẽ nhé
a, Vì K thuộc đường tròn đường kính AB
=> AKB=90
Mà CHA=90
=> tứ giác AKNH nội tiếp
Vậy tứ giác AKNH nội tiếp
b,Vì 2 tiếp tuyến cắt nhau tại M
nên \(OM\perp AC\)
=>\(OM//CB\)
=> tam giác AMO đồng dạng tam giác HCB
=> ĐPCM
c, Tứ giác AMKI nội tiếp do AIM=AKM=90
KIC=AMK
MÀ AMK=KNC do AM song song CH
=> KIC=KNC
=> tứ giác KINC nội tiếp
=>KNI=KCI
Mà KCI=KBA
=> KNI=KBA
=> IN song song AB
Vậy IN song song AB
Mình không viết kí hiệu góc nên bạn thông cảm

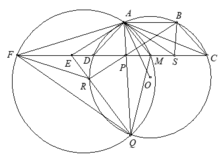
2). Vì EA là tiếp xúc (O) và từ kết quả câu 1) ta có E A 2 = E R . E Q = E P 2 .
Từ đó có E A = E P ⇒ D A P ^ = E A P ^ − E A D ^ = A P E ^ − A C D ^ = P A C ^
Do đó AP là phân giác D A C ^ ⇒ Q C = Q D ⇒ Q M ⊥ C D

A B C O I M N P Q L K J
Đặt bán kính của (I) và (O) lần lượt là \(r\) và \(R\).Gọi AI cắt (O) tại K khác A, KO cắt PQ, (O) lần lượt tại J,L.
Dễ thấy K là điểm chính giữa cung PQ và BC, suy ra KP = KQ, cũng dễ có KM = KN (1)
Áp dụng ĐL Cosin vào \(\Delta\)AKN ta có:
\(KN^2=AK^2+AN^2-2AK.AN.\cos45^0\Rightarrow KN^2=2R^2+2Rr+r^2\) (2)
Ta thấy OJ có độ dài bằng một nửa đường cao AH của \(\Delta\)ABC. Từ ĐL Ptolemy và Thales ta tính được:
\(AH=r.\frac{AB+AC+2R}{2R}=\frac{2Rr+r^2}{R}\Rightarrow OJ=\frac{2Rr+r^2}{2R}\)
Áp dụng hệ thức lượng tam giác vuông có:
\(KQ^2=KJ.KL=\left(R+\frac{2Rr+r^2}{2R}\right).2R=2R^2+2Rr+r^2\) (3)
Từ (1),(2) và (3) suy ra KM = KN = KP = KQ. Điều đó có nghĩa là M,N,P,Q cùng thuộc đường tròn tâm K (đpcm).

T M P I 3
gọi T ;P là 2 tiếp điểm của 2 tiếp tuyến kẻ từ M đến đường tròn (C)
\(\Delta MTP\) cận tại M (t/c tt)\(\Rightarrow MO\) là tia phân giác ;đường cao ...
\(\Rightarrow\widehat{TMO}=\widehat{PMO}=60^0\left(gt\right)\)
\(\Delta TMO\) có \(\widehat{MTO}=90^0\left(tt\right)\)\(\Rightarrow\Delta TMO\) là tam giác nửa đều
\(\Rightarrow MO=2TO=2.3=6\)
vậy tập hợp những điểm M cách đều điểm I(1;2) 1 khoảng cố định=6 là đường tròn tâm I(1;2) và bán kính R=6.
PT duong tron (C') \(\left(x-1\right)^2+\left(y-2\right)^2=36\).

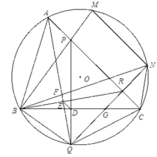
2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q