K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
1 tháng 2 2017
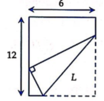
Thể tích hình lăng lớn nhất khi và chỉ khi diện tích ΔABC lớn nhất.
Gọi độ dài BC là x (m). Kẻ AH ⊥ BC.
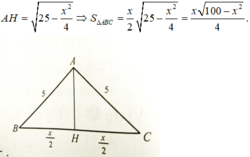
Bài toán đưa về tìm x ∈ (0; 10) để hàm số y = x√(100-x2) có giá trị lớn nhất.
Ta có:
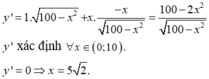
Bảng biến thiên:
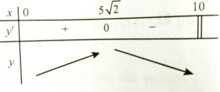
Hàm số đạt giá trị lớn nhất tại x = 5 2 ≈ 7 .
Chọn đáp án B.
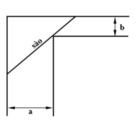
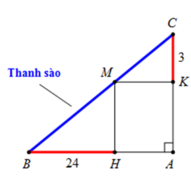




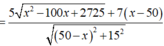

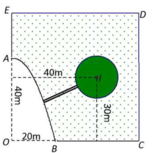
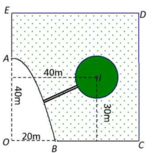

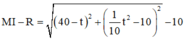
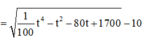
Theo bài ra, thanh sào sẽ đi qua các điểm B, M , C (hình vẽ dưới)
Suy ra độ dài thanh sào là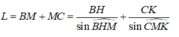
Đặt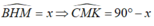 ,do đó
L
=
24
sin
x
+
3
cos
x
,do đó
L
=
24
sin
x
+
3
cos
x
Yêu cầu bài toán ⇔ L m i n ⇔ f ( x ) = 24 sin x + 3 cos x m i n
Ta có f ' ( x ) = 3 sin x cos 2 x - 24 cos x sin 2 x = 0 ⇔ sin 3 x = 8 cos 3 x ⇔ tan x = 2 ⇒ cos x = 1 1 + tan 2 x = 1 5 ⇒ sin x = 1 - cos 2 x = 2 5
Suy ra m i n ( 0 ; π 2 ) f ( x ) = 15 5 . Vậy độ dài tối thiểu của thanh sào là 15 5
Chọn C.