Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)45 = 32.5
204 = 22.3.17
126 = 2.32.7
=> UCLN(a;b;c) = 3
b)có BCNN(a;b;c) = 22.32.5.7.17 = 21420
=>BCNN:UCLN=21420:3=7140
=> BCNN chia hết cho UCLN
HT

câu a; b cách làm tương tự nhau. Bạn xem câu ở câu hỏi tương tự: http://olm.vn/hoi-dap/question/89869.html
c) đề bài cho [a;b] + (a;b) = 15
gọi d = (a;b) => a = d.m; b = d.n ( coi m < n và m; n nguyên tố cùng nhau)
Ta có: [a;b] = \(\frac{a.b}{d}=\frac{dm.dn}{d}=d.m.n\)
khi đó, d.mn + d = 15 => d(m.n + 1) = 15 => m.n + 1 \(\in\) Ư(15) mà m.n + 1 > 2
=> m.n + 1 \(\in\) {3;5;15}
+) m.n + 1 = 3 => m.n = 2 = 1.2 => m = 1; n = 2 và d = 5 => a = 5.1 = 5; b = 5.2 = 10
+) m.n + 1 = 5 => m.n = 4 = 1.4 => m = 1; n = 4 và d = 3 => a = 3.1 = 3; b = 3.4 = 12
+) m.n + 1 = 15 => m.n = 14 =1 .14 = 2.7
m =1; n = 14 ; d = 1 => a= 1; b = 14
m = 2; n = 7 ;d = 1 => a = 2; b = 7
Vậy....

câu trả lời là mới hok lp 5 sang năm lên lp 6 :)
Gọi 2 số đó là a và b, ƯCLN(a,b)=d
=>a=da'
b=db'
(a',b')=1
BCNN(a,b)=da'b'
Tổng ƯCLN và BCNN là d+da'b'=d(a'b'+1)=126
126 phân tích ra thừa số nguyên tố là 2.32.7
Do đó d=2 hoặc a'b'+1=2
Nếu d=2 thì a'b'+1=126:2=63
a'b'=62. Giả sử a>b thì a'>b'
TH1: a'=31, b'=2 =>a=31.2=62, b=2.2=4. a-b=58
TH2 a'=62, b'=1 =>a=62.2=124, b=2. a-b=122.
Hiệu nhỏ nhất nếu d=2 là 58
Tiếp theo ta xét
a'b'+1=2
a'b=1
=>a'=b'=1
Khi đó d=126:2=63
Ta có a=63, b=63
a-b=0
Tuy nhiên đề bài yêu cầu tìm hiệu dương mà số 0 ko dương cũng ko âm
Vậy 2 số cần tìm là 62 và 4

Bài 15. a) Tìm sáu bội của 6 ; b) Tìm các bội nhỏ hơn 30 của 7.
a) 6 bội của 6 là : {0 ; 6 ; 12 ; 18 ; 24 ; 30}
b) bội nhỏ hơn 30 của 7 là : {0 ; 7 ; 14 ; 21 ; 28}
Bài 16. a) Tìm tất cả các ước của 36 ; b) Tìm các ước lớn hơn 10 của 100
a) Ư(36) = {1 ; 2 ; 3 ; 4 ;6 ; 9 ; 12 ; 18}
b) Ư(100) = {20 ; 25 ; 50}
Bài 17. Tìm số tự nhiên x , biết a) x là bội của 11 và 10 x 50 . b) x vừa là bội của 25 vừa là ước của 150.
a) vậy x E BC(11 và 500) vì 11 và 500 nguyên tố cùng nhau nên BC(11 ; 500) = 500 x 11 = 5500
vậy x \(⋮\)25 và 150 \(⋮\)x B(25) = {0 ; 25 ; 50 ; 75 ; 100 ; 125 ; 150 ; 175...}
Ư(150) = {1 ; 2 ; 3 ; 5 ; 6 ; 10 ; 15 ; 25 ; 30 ; 50 ; 75 ; 150} => a = (25 ; 50 ; 75)
Bài 18. Trong các số: 4827,5670,6915,2007 , số nào: a) chia hết cho 2 ? b) chia hết cho 3 ? c) chia hết cho 5 ? d) chia hết cho 9 ?
a) chia hết cho 2 là : 5670
b) chia hết cho 3 là : 2007 ; 6915 ; 5670 ; 4827
c) chia hết cho 5 là : 5670 ; 6915
d) chia hết cho 9 là : 2007 ;
Bài 19. Trong các số sau: 0,12,17,23,110,53,63,31 , số nào là số nguyên tố?
SNT là : 17 ; 23 ; 53 ; 31
Bài 20. Thay dấu * bằng chữ số thích hợp để mỗi số sau là số nguyên tố: a) 4* b) 7*, c) * d) 2*1
4* = 41 ; 43 ; 47
7* = 71 ; 73 ; 79
* = 2 ; 3 ; 5 ; 7
2*1 ; 221 ; 211 ; 251 ; 271
Bài 21. Thay dấu * bằng chữ số thích hợp để mỗi số sau là hợp số: a) 1* ; b) * 10 c) *1 d) *73.
1* = 11 ; 13 ; 17 ; 19
*10 = ???
*1 = 11 ; 31 ; 41 ; 61 ; 71 ; 91
*73 = 173 ; 373 ; 473 ; 673 ; 773 ; 973

1)a chia hết cho b thì b là ước của a
a chia hết cho b thì b là bội của a.
2)Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
3)Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
4)Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
5)Ước chung của hai hay nhiều số là ước của tất cả các số đó.
6) Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
7)ƯCLN của hai hay nhiều số là số lơn nhất trong tập hợp ước chung
9)Bội chung của hai hay nhiều số là bội của tất cả các số đó.
10

1)a chia hết cho b thì b là ước của a
a chia hết cho b thì b là bội của a.
2)Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
3)Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
4)Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
5)Ước chung của hai hay nhiều số là ước của tất cả các số đó.
6) Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
7)ƯCLN của hai hay nhiều số là số lơn nhất trong tập hợp ước chung
9)Bội chung của hai hay nhiều số là bội của tất cả các số đó.
10

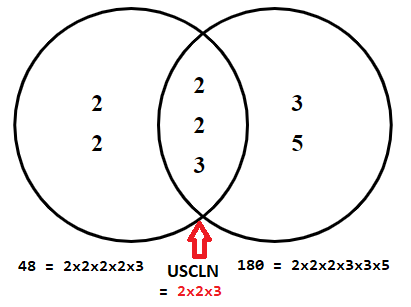
2.2.3=12.USCLN (12) :2;3;4;6;12;1
BSCLN:(1;2;3...............)
Chúc bạn học tốt nha
TL:
2.2.3=12.USCLN (12) :2;3;4;6;12;1
BSCLN:(1;2;3...............)
^H T^