Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Anh Vi Cá Đuối: Biểu thức A thì biến là $x,y$. Mà đề bài thì $x_1,x_2$???

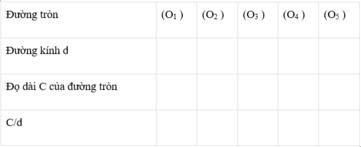
| Đường tròn | (O1 ) | (O2 ) | (O3 ) | (O4 ) | (O5 ) |
| Đường kính d | 2 | 3 | 4 | 5 | 6 |
| Đọ dài C của đường tròn | 6,4 | 9,5 | 12,6 | 15,5 | 18,9 |
| C/d | 3,2 | 3,167 | 3,15 | 3,1 | 3,15 |
e) Ta có 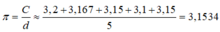
Nhận xét: Ta chỉ ước lượng được giá trị gần đúng của số π

1, Phương trình hoành độ giao điểm của \(\left(P\right)\)và \(\left(d\right)\)là:
\(-x^2=mx-1\)
\(\Leftrightarrow x^2+mx-1=0\)(1)
Phương trình có hệ số \(a.c=1.\left(-1\right)=-1< 0\)nên luôn có hai nghiệm phân biệt.
Do đó \(\left(P\right)\)luôn cắt \(\left(d\right)\)tại hai điểm phân biệt \(A,B\).
2, Phương trình (1) luôn có hai nghiệm phân biệt \(x_1,x_2\).
Theo định lí Viete ta có:
\(\hept{\begin{cases}x_1+x_2=-m\\x_1x_2=-1\end{cases}}\)
\(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=-m^3-3.\left(-1\right).\left(-m\right)\)
\(=-m^3-3m=-4\)
\(\Leftrightarrow m^3+3m-4=0\)
\(\Leftrightarrow\left(m-1\right)\left(m^2+m+4\right)=0\)
\(\Leftrightarrow m-1=0\)(vì \(m^2+m+4=m^2+m+\frac{1}{4}+\frac{15}{4}=\left(m+\frac{1}{2}\right)^2+\frac{15}{4}>0\))
\(\Leftrightarrow m=1\).

a) Chứng minh tích BD.CEBD.CE không đổi.
Xét hai tam giác: ΔBOD∆BOD và ΔCEO∆CEO, ta có: ˆB=ˆC=600B^=C^=600 (gt) (1)
Ta có ˆDOCDOC^ là góc ngoài của ΔBDO∆BDO nên: ˆDOC=ˆB+ˆD1DOC^=B^+D^1
hay ˆO1+ˆO2=ˆB+ˆD1⇔600+ˆO2=600+ˆD1O1^+O2^=B^+D1^⇔600+O2^=600+D1^
⇔ˆO2=ˆD1(2)⇔O2^=D1^(2)
Từ (1) và (2) ⇒ΔBOD⇒∆BOD đồng dạng ΔCEO∆CEO (g.g)
⇒BDBO=COCE⇒BD.CE=BO.CO⇒BDBO=COCE⇒BD.CE=BO.CO
hay BD.CE=BC2.BC2=BC24BD.CE=BC2.BC2=BC24 (không đổi)
Vậy BD.CE=BC24BD.CE=BC24 không đổi
b) Chứng minh ΔBODΔBOD đồng dạng ΔOEDΔOED
Từ câu (a) ta có: ΔBOD∆BOD đồng dạng ΔCEO∆CEO
⇒ODOE=BDOC=BDOB⇒ODOE=BDOC=BDOB (do OC=OBOC=OB)
Mà ˆB=ˆDOE=600B^=DOE^=600
Vậy ΔBODΔBOD đồng dạng ΔOEDΔOED (c.g.c) ⇒ˆBDO=ˆODE⇒BDO^=ODE^
hay DODO là tia phân giác của góc BDEBDE
c) Vẽ OK⊥DEOK⊥DE và gọi II là tiếp điểm của (O)(O) với ABAB, khi đó OI⊥ABOI⊥AB. Xét hai tam giác vuông: IDOIDO và KDOKDO, ta có:
DODO chung
ˆD1=ˆD2D1^=D2^ (chứng minh trên)
Vậy ΔIDOΔIDO = ΔKDOΔKDO⇒OI=OK⇒OI=OK
Điều này chứng tỏ rằng OKOK là bán kính của (O)(O) và OK⊥DEOK⊥DE nên KK là tiếp điểm của DEDE với (O)(O)hay DEDE tiếp xúc với đường tròn (O)

\(A=\left(\sqrt{5}-1\right)\frac{5+\sqrt{5}}{2\sqrt{5}}=\frac{\sqrt{5}\left(5-1\right)}{2\sqrt{5}}=2\)
\(B=\frac{4}{\sqrt{x}+2}-\frac{\sqrt{x}-6}{x+2\sqrt{x}}=\frac{4\sqrt{x}-\sqrt{x}+6}{\sqrt{x}\left(\sqrt{x}+2\right)}=\frac{3\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
Cho đường tròn (O;R), dây BC cố định và #Hỏi cộng đồng OLM #Toán lớp 9

Sorry chị nha , em mới học lớp 4 nên ko giải đc