Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số \(x^{\dfrac{3}{5}}\) xác định \(\Leftrightarrow x>0\)
\(\Rightarrow D\)

Điều kiện xác định: \(x^2-2x+1>0\)
Mà \(x^2-2x+1=\left(x-1\right)^2\ge0\forall x\in R\)
\(\Rightarrow x-1\ne0\\ \Leftrightarrow x\ne1\)
Vậy D = \(R/\left\{1\right\}\) ⇒ Chọn B.

À cái kết luận đó liên quan tới lý thuyết đồ thị của các hàm bậc 3 mà lên lớp 12 mới học nên bạn thấy hơi lạ là đúng rồi :(
Bạn cứ hiểu hàm bậc 3 p(x) là một hàm mà miền giá trị của nó luôn chạy từ \(\left(-\infty;+\infty\right)\) bất chấp các hệ số A, B, C, D bằng bao nhiêu, do đó luôn chọn được 1 giá trị x nào đó sao p(x) nằm trên miền dương.
Đồng thời khi A<0 thì ta có \(\lim\limits_{x\rightarrow+\infty}p\left(x\right)=-\infty\) nên luôn tồn tại 1 giá trị x đủ lớn làm cho p(x) âm.
Hay bạn cứ nghĩ đơn giản cho A, B, C, D các giá trị bất kì trong đó A<0, rồi cho x một giá trị lớn cỡ vài tỉ thì kiểu gì p(x) cũng âm
Bạn cần ghi đầy đủ bài toán, ghi thiếu thế này thì chịu thua thôi bạn ạ

Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\), \(f\left( x \right) = \frac{{{x^2} - 2x}}{x}\) là hàm phân thức hữu tỉ nên liên tục trên từng khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Ta có: \(f\left( 0 \right) = a\)
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2} - 2x}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{x\left( {x - 2} \right)}}{x} = \mathop {\lim }\limits_{x \to 0} \left( {x - 2} \right) = 0 - 2 = - 2\)
Để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại điểm \({x_0} = 0\). Khi đó:
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow a = - 2\).
Vậy với \(a = - 2\) thì hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
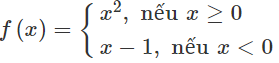
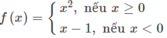
Hàm số \(x^{-3}\) xác định \(\Leftrightarrow x\ne0\)
\(\Rightarrow C\)