Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ pt li độ, ta thấy \(A=4cm;\omega=20\left(rad/s\right);\varphi_0=\dfrac{2}{3}\pi\left(rad\right)\) \(\Rightarrow T=\dfrac{2\pi}{\omega}=\dfrac{\pi}{10}\left(s\right)\)
Đường tròn lượng giác:
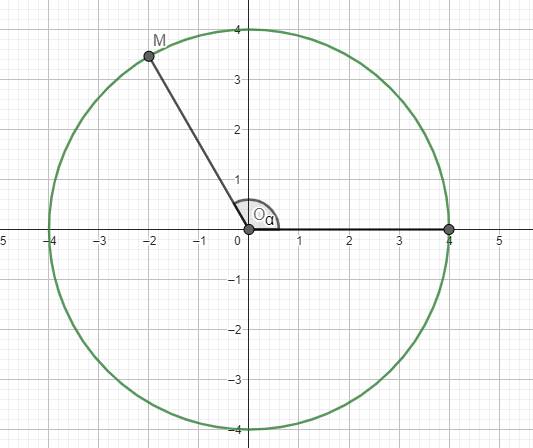
Trong thời gian từ 0 đến 6 giây, góc quét của vật là \(\Delta\varphi=2\pi.\dfrac{\Delta t}{T}=2\pi.\dfrac{6}{\dfrac{\pi}{10}}=120\left(rad\right)\)
(Tới đây bạn chỉ cần đếm xem vật quét \(120rad\) thì qua VTCB bao nhiêu lần là được)

Vận tốc của vật vào thời điểm đó là: \(v=A\omega=\dfrac{2\pi A}{T}=\dfrac{2\pi\cdot10}{2}=10\pi\left(cm/s\right)\)

a)Chu kì: \(T=2\pi\cdot\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,2}{200}}=0,2s\Rightarrow\omega=\dfrac{2\pi}{T}=10\pi\)
Vật qua vị trí \(x=1,5=\dfrac{A}{2}\) theo chiều dương nên \(\varphi=-\dfrac{\pi}{3}\).
PT dao động của vật: \(x=Acos\left(\omega t+\varphi\right)=3cos\left(10\pi-\dfrac{\pi}{3}\right)\left(cm\right)\)
b)Tại \(t=1s\) thì:
Vận tốc vật:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi\cdot3\cdot sin\left(10\pi t-\dfrac{\pi}{3}\right)=-30\pi sin\left(10\pi t-\dfrac{\pi}{3}\right)\)
\(\Rightarrow v=-30\pi sin\left(10\pi\cdot1-\dfrac{\pi}{3}\right)\approx81,62cm/s\)
Gia tốc vật:
\(a=-\omega^2Acos\left(\omega t+\varphi\right)=-3000cos\left(10\pi t-\dfrac{\pi}{3}\right)\left(cm/s^2\right)\)
\(\Rightarrow a=-3000cos\left(10\pi\cdot1-\dfrac{\pi}{3}\right)=-1500\left(cm/s^2\right)\)

\(x=10Cos5t\rightarrow A=10cm,\omega=5\left(\dfrac{rad}{s}\right),\varphi=0\)
Khi t = 2 --> pha dao động : \(5.2=10\left(rad\right)\)
Tại vị trí cân bằng vận tốc có giá trị cực đại : \(v_{max}=\omega A=5.10=50\left(\dfrac{cm}{s}\right)\)

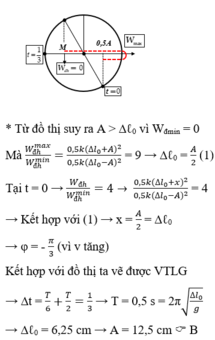
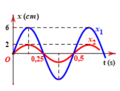

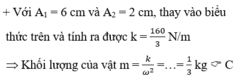
`T=pi/10(s)=> \omega =20 (rad//s)`
`@A=\sqrt{2^2 +[(40\sqrt{3})^2]/[20^2]}=4(cm)`
Vì tại thời điểm `t=\pi/10` trùng với thời điểm `t=0`
`=>{(x=2(cm)),(v=40\sqrt{3}(cm//s)),(a=-\omega ^2 .x=-800(cm//s^2)):}`