Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 2: Để hệ có nghiệm duy nhất thì \(\frac{1}{a}<>\frac{a}{1}\)
=>\(a^2<>1\)
=>a∉{1;-1](1)
\(\begin{cases}ax+y=3a\\ x+ay=2a+1\end{cases}\Rightarrow\begin{cases}y=3a-ax\\ x+a\left(3a-ax\right)=2a+1\end{cases}\)
=>\(\begin{cases}y=3a-a\cdot x\\ x+3a^2-a^2\cdot x=2a+1\end{cases}\Rightarrow\begin{cases}y=3a-ax\\ x\left(1-a^2\right)=2a+1-3a^2\end{cases}\)
=>\(\begin{cases}x=\frac{-3a^2+2a+1}{1-a^2}=\frac{3a^2-2a-1}{a^2-1}=\frac{\left(a-1\right)\left(3a+1\right)}{\left(a-1\right)\left(a+1\right)}=\frac{3a+1}{a+1}\\ y=3a-a\cdot\frac{3a+1}{a+1}=\frac{3a^2+3a-3a^2-a}{a+1}=\frac{2a}{a+1}\end{cases}\)
Để x,y nguyên thì \(\begin{cases}3a+1\vdots a+1\\ 2a\vdots a+1\end{cases}\Rightarrow\begin{cases}3a+3-2\vdots a+1\\ 2a+2-2\vdots a+1\end{cases}\)
=>-2⋮a+1
=>a+1∈{1;-1;2;-2}
=>a∈{0;-2;1;-3}
Kết hợp (1), ta có: a∈{0;-2;-3}
Bài 3:
ĐKXĐ: x>=y
\(\begin{cases}\sqrt{\frac{x+y}{2}}+\sqrt{\frac{x-y}{3}}=14\\ \sqrt{\frac{x+y}{8}}-\sqrt{\frac{x-y}{12}}=3\end{cases}\Rightarrow\begin{cases}\sqrt{\frac{x+y}{2}}+\sqrt{\frac{x-y}{3}}=14\\ \frac12\left(\sqrt{\frac{x+y}{2}}-\sqrt{\frac{x-y}{3}}\right)=3\end{cases}\)
=>\(\begin{cases}\sqrt{\frac{x+y}{2}}+\sqrt{\frac{x-y}{3}}=14\\ \sqrt{\frac{x+y}{2}}-\sqrt{\frac{x-y}{3}}=6\end{cases}\Rightarrow\begin{cases}\sqrt{\frac{x+y}{2}}=10\\ \sqrt{\frac{x-y}{3}}=4\end{cases}\)
=>\(\begin{cases}\frac{x+y}{2}=100\\ \frac{x-y}{3}=16\end{cases}\Rightarrow\begin{cases}x+y=200\\ x-y=48\end{cases}\Rightarrow\begin{cases}x=\frac{200+48}{2}=\frac{248}{2}=124\\ y=200-124=76\end{cases}\) (nhận)
a, Ta có tam giác \(A B C\) nhọn, kẻ:
- \(B D \bot A B\)
- \(C D \bot A C\)
=> Các góc tại \(B\) và \(C\) đều là góc vuông.
Ta xét tứ giác \(A B D C\):
- \(\angle A B D = 90^{\circ}\) (do \(B D \bot A B\))
- \(\angle A C D = 90^{\circ}\) (do \(C D \bot A C\))
Suy ra:
\(\angle A B D + \angle A C D = 180^{\circ}\)
Mà tổng góc trong tứ giác bằng \(360^{\circ}\), nên:
\(\angle B A D + \angle B C D + 180^{\circ} = 360^{\circ} \Rightarrow \angle B A D + \angle B C D = 180^{\circ}\)
Mà \(\angle B A D\) chính là góc tại \(A\) của tam giác \(A B C\), ký hiệu là \(\angle A\),
\(\angle B C D\) chính là góc tại \(D\) trong tứ giác (ký hiệu là \(\angle D\)).
⇒ \(\Rightarrow \angle D + \angle A = 180^{\circ}\)
b, * Chứng minh \(Q J = B D\)
Vì \(I\) là trung điểm của \(P Q\) và \(B J\), nên:
- \(I P = I Q\) (trung điểm \(P Q\))
- \(I B = I J\) (trung điểm \(B J\))
Xét hai tam giác \(I P B\) và \(I Q J\):
- \(I P = I Q\) (gt)
- \(I B = I J\) (gt)
- \(\angle P I B = \angle Q I J\) (đối đỉnh)
⇒ Tam giác \(I P B\) ≅ tam giác \(Q I J\) (cạnh – cạnh – góc xen giữa)
Suy ra:
\(P B = Q J\)
Nhưng \(P B = A B - A P = A B - \left(\right. A B - B P \left.\right) = B P\), mà \(B P = B D\) (gt)
⇒ \(Q J = P B = B P = B D \Rightarrow \boxed{Q J = B D}\)
*Chứng minh \(\angle A Q J + \angle D = 180^{\circ}\)
Ta đã biết ở phần a): \(\angle A + \angle D = 180^{\circ} .\)
Ta sẽ chứng minh \(\angle A Q J = \angle A\)
Xét hai tam giác:
- Tam giác \(A B P\): có \(B P = B D\) (gt)
- Tam giác \(A C Q\): có \(C Q = C D\) (gt)
Do \(B D \bot A B\), \(C D \bot A C\) ⇒ \(B D\) là đường cao tam giác \(A B C\), tương tự \(C D\) cũng là đường cao.
Suy ra tam giác \(A B P\) vuông tại \(B\), tam giác \(A C Q\) vuông tại \(C\). Hai điểm \(P , Q\) được lấy đối xứng vai trò như nhau theo hai cạnh của tam giác \(A B C\).
Lại có \(Q J = B D = B P\) (ở trên vừa chứng minh), do đó tam giác \(A Q J\) đồng dạng với tam giác \(A B C\) ⇒
\(\angle A Q J = \angle A .\)
Vậy:
\(\angle A Q J + \angle D = \angle A + \angle D = 180^{\circ} . \textrm{ }\textrm{ } \textrm{ } (đ\text{pcm})\)
Vậy cái điều kiện \(x\ne\sqrt{3}\)người ta cho chi bạn. Bạn nên để ý là cái điều kiện người ta cho là nhằm cho cái đó nó xác định chớ không cho tào lao đâu. x # 0 cũng là vì lý do đó nên mình chắc cái đề trong sách in sai
Với điều kiện kèm theo thì mình chắc rằng cái đề phải là x - \(\sqrt{27}\) chứ không thể lad x - 27 được. Bạn xem lại đề nhé
@hieu nguyen Em có nhân chéo hai vế và khai triển ra nhưng cũng không ra cái gì ạ.
a. Câu này đơn giản em tự giải
b.
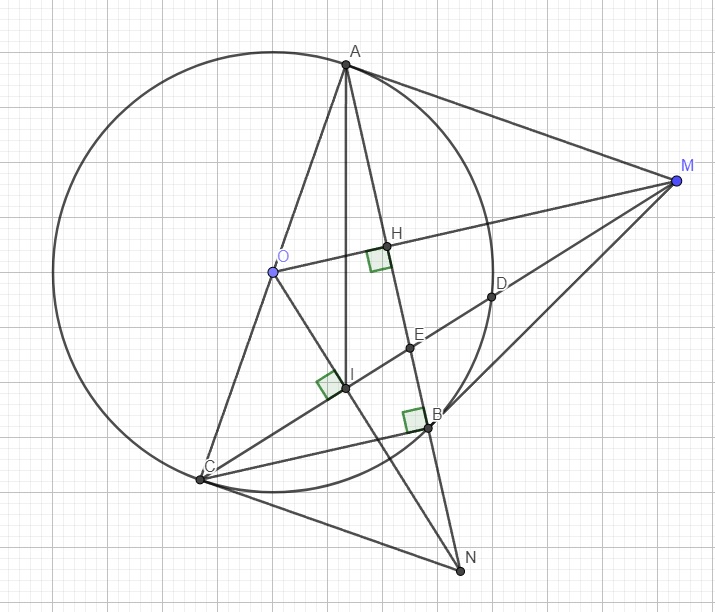
Xét hai tam giác OIM và OHN có:
\(\left\{{}\begin{matrix}\widehat{OIM}=\widehat{OHN}=90^0\\\widehat{MON}\text{ chung}\\\end{matrix}\right.\) \(\Rightarrow\Delta OIM\sim\Delta OHN\left(g.g\right)\)
\(\Rightarrow\dfrac{OI}{OH}=\dfrac{OM}{ON}\Rightarrow OI.ON=OH.OM\)
Cũng từ 2 tam giác đồng dạng ta suy ra \(\widehat{OMI}=\widehat{ONH}\)
Tứ giác OAMI nội tiếp (I và A cùng nhìn OM dưới 1 góc vuông)
\(\Rightarrow\widehat{OAI}=\widehat{OMI}\)
\(\Rightarrow\widehat{OAI}=\widehat{ONH}\) hay \(\widehat{OAI}=\widehat{ONA}\)
c.
Xét hai tam giác OAI và ONA có:
\(\left\{{}\begin{matrix}\widehat{OAI}=\widehat{ONA}\left(cmt\right)\\\widehat{AON}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAI\sim\Delta ONA\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{ON}=\dfrac{OI}{OA}\Rightarrow OI.ON=OA^2=OC^2\) (do \(OA=OC=R\))
\(\Rightarrow\dfrac{OC}{ON}=\dfrac{OI}{OC}\)
Xét hai tam giác OCN và OIC có:
\(\left\{{}\begin{matrix}\dfrac{OC}{ON}=\dfrac{OI}{OC}\\\widehat{CON}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OCN\sim\Delta OIC\left(g.g\right)\)
\(\Rightarrow\widehat{OCN}=\widehat{OIC}=90^0\) hay tam giác ACN vuông tại C
\(\widehat{ABC}\) là góc nt chắn nửa đường tròn \(\Rightarrow BC\perp AB\)
Áp dụng hệ thức lượng trong tam giác vuông ACN với đường cao BC:
\(BC^2=BN.BA=BN.2BH=2BN.BH\) (1)
O là trung điểm AC, H là trung điểm AB \(\Rightarrow OH\) là đường trung bình tam giác ABC
\(\Rightarrow OH=\dfrac{1}{2}BC\)
Xét hai tam giác OHN và EBC có:
\(\left\{{}\begin{matrix}\widehat{OHN}=\widehat{EBC}=90^0\\\widehat{ONH}=\widehat{ECB}\left(\text{cùng phụ }\widehat{IEB}\right)\end{matrix}\right.\) \(\Rightarrow\Delta OHN\sim\Delta EBC\left(g.g\right)\)
\(\Rightarrow\dfrac{OH}{EB}=\dfrac{HN}{BC}\Rightarrow HN.EB=OH.BC=\dfrac{1}{2}BC^2\)
\(\Rightarrow BC^2=2HN.EB\) (2)
(1);(2) \(\Rightarrow BN.BH=HN.BE\)
\(\Rightarrow BN.BH=\left(BN+BH\right).BE\)
\(\Rightarrow\dfrac{1}{BE}=\dfrac{BN+BH}{BN.BH}=\dfrac{1}{BH}+\dfrac{1}{BN}\) (đpcm)
Bài 4:
a: ΔCAB vuông tại C
=>\(\hat{CAB}+\hat{CBA}=90^0\)
=>\(\hat{CBA}=90^0-70^0=20^0\)
Xét ΔCBA vuông tại C có \(\sin CBA=\frac{CA}{AB}\)
=>\(CA=AB\cdot\sin CBA=10\cdot\sin20\) ≃3,4(dm)
ΔCAB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(CB^2=AB^2-CA^2\)
=>\(CB=\sqrt{AB^2-AC^2}\) ≃9,4(dm)
b: Xét ΔABC vuông tại C có \(cosA=\frac{CA}{AB}\)
Xét ΔCHA vuông tại H có \(cosA=\frac{AH}{AC}\)
Xét ΔCHB vuông tại H có \(\sin B=\frac{CH}{CB}\)
Xét ΔCAB vuông tại C có \(\sin B=\frac{AC}{AB}\)
\(\sin B\cdot cosA=\frac{AC}{AB}\cdot\frac{AH}{AC}=\frac{AH}{AB}\)
Bài 5:
Xét ΔMAB có \(\hat{MBH}\) là góc ngoài tại đỉnh B
nên \(\hat{MBH}=\hat{A}+\hat{BMA}\)
=>\(\hat{BMA}=39^0-18^0=21^0\)
Xét ΔMAB có \(\frac{AB}{\sin AMB}=\frac{MB}{\sin A}\)
=>\(\frac{MB}{\sin18}=\frac{80}{\sin21}\)
=>\(MB=80\cdot\frac{\sin18}{\sin21}\) ≃69(m)
Xét ΔMHB vuông tại H có \(\sin HBM=\frac{HM}{MB}\)
=>\(HM=MB\cdot\sin HBM\) ≃69*sin39≃43,4(m)
=>Chiều cao của ngọn hải đăng là khoảng 43,4 mét
\(A=\dfrac{2\left(3+\sqrt{5}\right)}{4+\sqrt{6+2\sqrt{5}}}+\dfrac{2\left(3-\sqrt{5}\right)}{4-\sqrt{6-2\sqrt{5}}}=\dfrac{2\left(3+\sqrt{5}\right)}{4+\sqrt{\left(\sqrt{5}+1\right)^2}}+\dfrac{2\left(3-\sqrt{5}\right)}{4-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\dfrac{2\left(3+\sqrt{5}\right)}{5+\sqrt{5}}+\dfrac{2\left(3-\sqrt{5}\right)}{5-\sqrt{5}}=\dfrac{2\left(3+\sqrt{5}\right)\left(5-\sqrt{5}\right)+2\left(3-\sqrt{5}\right)\left(5+\sqrt{5}\right)}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)
\(=\dfrac{40}{20}=2\)
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2