Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBEM vuông tại E và ΔBKM vuông tại K có
BM chung
góc KBM=góc EBM
=>ΔBEM=ΔBKM
=>ME=MK
b: Xét ΔCKM vuông tại K và ΔCFM vuông tại F có
CM chung
góc KCM=góc FCM
=>ΔCKM=ΔCFM
=>MK=MF=ME
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ME=MF
=>ΔAEM=ΔAFM
=>góc EAM=góc FAM
=>AM là phân giác của góc BAC

4)
theo câu 2,ta có:\(\Delta ABM=\Delta CDM\left(g.cg\right)\)
\(\Rightarrow AB=CD\Rightarrow\frac{1}{2}AB=\frac{1}{2}CD=IB=BA=CK=KD\)
xét \(\Delta\) AIM và \(\Delta\)CKM có:
AI=CK(cmt)
AM=MC(gt)
góc IAM=góc MCK=\(90^o\)
=>\(\Delta AIM=\Delta CKM\left(c.g.c\right)\)
\(\Rightarrow\widehat{IMA}=\widehat{CMK}\) => M là giao điểm của IK và AC
=> I,M,K thẳng hàng

Câu 1: Em tham khảo tại đây nhé.
Câu hỏi của trần thị minh hải - Toán lớp 7 - Học toán với OnlineMath
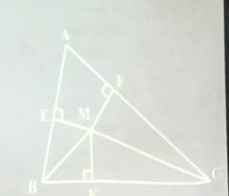



a: Xét ΔBEM vuông tại E và ΔBKM vuông tại K có
BM chung
góc EBM=góc KBM
=>ΔBEM=ΔBKM
=>ME=MK
b: Xét ΔCKM vuông tại K và ΔCFM vuông tại F có
CM chung
góc KCM=góc FCM
=>ΔCKM=ΔCFM
=>MK=MF
=>ME=MF
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
MF=ME
=>ΔAEM=ΔAFM
=>góc EAM=góc FAM
=>AM là phân giác của góc BAC