
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
TXĐ: \(D=R\backslash\left\{-2\right\}\)
Sự biến thiên: \(y'=\dfrac{5}{\left(x+2\right)^2}>0\) ; \(\forall x\ne-2\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-2\right)\) và \(\left(-2;+\infty\right)\)
\(\lim\limits_{x\rightarrow-2}\dfrac{3x+1}{x+2}=\infty\Rightarrow x=-2\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow\infty}\dfrac{3x+1}{x+2}=3\Rightarrow y=3\) là tiệm cận ngang
Bảng biến thiên:
x y' y -2 -vc +vc + + 3 +vc -vc 3
b.
\(y'\left(-1\right)=\dfrac{5}{\left(-1+2\right)^2}=5\) ; \(y\left(-1\right)=\dfrac{3.\left(-1\right)+1}{-1+2}=-2\)
Phương trình tiếp tuyến:
\(y=5\left(x+1\right)-2\Leftrightarrow y=5x+3\)

HẾT RỒI NHÉ ĐÁP ÁN LÀ :
+ Ta có: y '= 3x2 + 6x + m
+ Để hàm số đã cho đồng biến trên R thì y' ≥ 0,∀x ∈R
+ Yêu cầu bài toán trở thành tìm điều kiện của m để y' ≥ 0,∀x ∈R
Ta có y' = 3x2 + 6x + m, ta có: a = 3>0,Δ = 36 - 12m
Để y' ≥ 0,∀x ∈ R khi Δ ≤ 0 ⇔ 36 - 12m ≤ 0 ⇔ m ≥ 3
Vậy giá trị của tham số m cần tìm là m ≥ 3

Chọn A.
Ta có
![]()
Suy ra
![]() .
.
Vì ![]()
nên hàm số đạt cực đại ![]() tại và giá trị cực đại là
tại và giá trị cực đại là ![]() .
.
Tương tự, ta có hàm số đạt cực tiểu tại ![]() và giá trị cực tiểu là
và giá trị cực tiểu là ![]() .
.
Ta giả sử điểm M là điểm cực đạ của đồ thị hàm số ứng với giá trị ![]() và là điểm cực tiểu ứng của đồ thị hàm số ứng với với giá trị
và là điểm cực tiểu ứng của đồ thị hàm số ứng với với giá trị ![]() .
.
Từ YCBT suy ra hệ phương trình
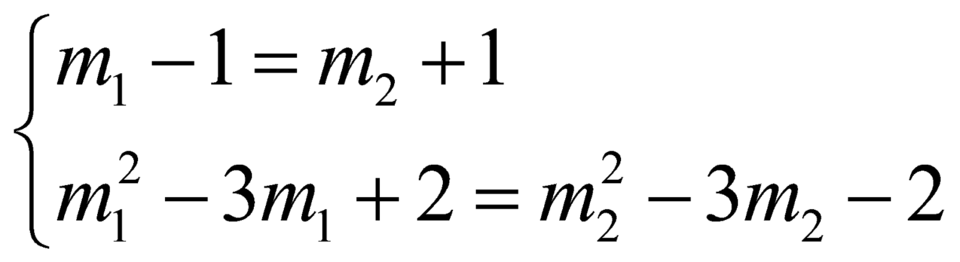
Giải hệ ta tìm được nghiệm ![]() và suy ra tồn tại duy nhất một điêm
và suy ra tồn tại duy nhất một điêm ![]() thỏa bài toán.
thỏa bài toán.

Với \(m=-2\) ko thỏa mãn
Với \(m\ne-2\) hàm \(f\left(x\right)\) là bậc nhất trên bậc nhất nên luôn đơn điệu trên khoảng đã cho
\(\Rightarrow\) min max rơi vào 2 đầu mút
\(f\left(2\right)=m+4\) ; \(f\left(3\right)=\dfrac{m+6}{2}\)
\(\Rightarrow\left|m+4-\dfrac{m+6}{2}\right|=2\Leftrightarrow\)
\(\Leftrightarrow m+2=\pm4\Rightarrow\left[{}\begin{matrix}m=2\\m=-6\end{matrix}\right.\)

Đáp án D
Phương pháp: Xét hai mặt phẳng
![]()
![]()
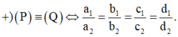
![]()
+) (P) và (Q) cắt nhau khi và chỉ khi chúng không song song hay trùng nhau.
![]()
Cách giải: Ta có: (P): 2x-y+3z-1=0 và (Q): 4x-2y+6z-1=0
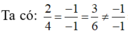
=> (P) và (Q) song song với nhau.

\(y'=\frac{\left(\frac{x+1}{-x+1}\right)}{1+\left(\frac{x+1}{-x+1}\right)^2}-\frac{1}{1+x^2}=\frac{2}{\left(1-x\right)^2}.\frac{\left(1-x\right)^2}{\left(1-x\right)^2+\left(x+1\right)^2}-\frac{1}{1+x^2}\)\(=\frac{2}{2\left(1+x^2\right)}-\frac{1}{1+x^2}=0;\forall x\ne1\)
- Xét \(x\in\left(-\infty,1\right):y'=0,\forall x\in\left(-\infty,1\right)\)nên y là hằng số trên \(\left(-\infty,1\right)\)
mà \(y\left(0\right)=arctg1-arctg0=\frac{\eta}{4}-0=\frac{\eta}{4}\Rightarrow y=\frac{\eta}{4},\forall x\in\left(-\infty,1\right)\)(n số pi ở đây không chắc là đúng chưa mình mở vô hộp có kí tự số pi rồi mà thấy kí tự có hơi lạ lạ, thông cảm nhá)
- Xét \(x\in\left(1,\infty\right):y'=0,\forall x\in\left(1,\infty\right)\)
\(\Rightarrow y\)là hằng số trên \(\left(1,\infty\right)\)
\(\Rightarrow arctg\left(\frac{1+x}{1-x}\right)-arctgx=k,\forall x\in\left(1,\infty\right)\)
Cho \(x\rightarrow\infty\)thì \(\left(\frac{1+x}{1-x}\right)\rightarrow-1:arctg\left(-1\right)-\frac{\eta}{2}=k\Rightarrow k=-\frac{\eta}{4}-\frac{\eta}{2}=-\frac{3\eta}{4}\)
Do đó \(y=-\frac{3\eta}{4},\forall x\in\left(1,\infty\right).\)
Vậy \(y=\hept{\begin{cases}\frac{\eta}{4}\left(neux< 1\right)\\-\frac{3\eta}{4}\left(neux>1\right)\end{cases}}\)nếu đó nha.
ko làm mà đòi có ăn thì ăn ĐB ăn cứt