Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án đúng là: D
Ta có: un+1 = 2n+1+1 = 2n+2
Xét hiệu un+1 – un = 2n+2 – 2n = 3.2n > 0 với mọi n ∈ ℕ*
Vậy dãy số đã cho là dãy số tăng.

1/ \(\lim\limits\dfrac{\dfrac{2^n}{7^n}-5.7.\left(\dfrac{7}{7}\right)^n}{\dfrac{2^n}{7^n}+\left(\dfrac{7}{7}\right)^n}=-35\)
2/ \(\lim\limits\dfrac{\dfrac{3^n}{7^n}-2.5.\left(\dfrac{5}{7}\right)^n}{\dfrac{2^n}{7^n}+\dfrac{7^n}{7^n}}=0\)
3/ \(\lim\limits\sqrt[3]{\dfrac{\dfrac{5}{n}-\dfrac{8n}{n}}{\dfrac{n}{n}+\dfrac{3}{n}}}=\sqrt[3]{-8}=-2\)

a) Ta có: \(n \ge 1\; \Rightarrow n - 1 \ge 0\; \Rightarrow {u_n} \ge 0,\;\forall \;n \in {N^*}\;\)
Do đó, \(\left( {{u_n}} \right)\) bị chặn dưới bởi 0.
\(\left( {{u_n}} \right)\) không bị chặn trên vì không tồn tại số M nào để \(n - 1 < M,\;\forall \;n \in {N^*}\).
b) Ta có:
\(\begin{array}{l}\forall n \in {N^*},{u_n} = \frac{{n + 1}}{{n + 2}} > 0.\\{u_n} = \frac{{n + 1}}{{n + 2}} = \frac{{n + 2 - 1}}{{n + 2}} = 1 - \frac{1}{{n + 2}} < 1,\forall n \in {N^*}\\ \Rightarrow 0 < {u_n} < 1\end{array}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn.
c) Ta có:
\( - 1 < \sin n < 1\)
\( \Rightarrow - 1 < {u_n} < 1,\forall n \in {N^*}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn.
d) Ta có:
Nếu n chẵn, \({u_n} = - {n^2} < 0\), \(\forall n \in {N^*}\).
Nếu n lẻ, \({u_n} = {n^2} > 0\), \(\forall n \in {N^*}\).
Vậy \(\left( {{u_n}} \right)\) không bị chặn.

\(u_n-u_{n+1}=u_n+\left(1-u_{n+1}\right)-1\ge2\sqrt{u_n\left(1-u_{n+1}\right)}-1>0\)
\(\Rightarrow u_n>u_{n+1}\Rightarrow\) dãy giảm
Dãy giảm và bị chặn dưới bởi 0 nên có giới hạn hữu hạn.
Gọi giới hạn đó là k
\(\Rightarrow k\left(1-k\right)\ge\dfrac{1}{4}\Rightarrow\left(2k-1\right)^2\le0\Rightarrow k=\dfrac{1}{2}\)
Vậy \(\lim\left(u_n\right)=\dfrac{1}{2}\)

a: \(\lim\limits\dfrac{5n+1}{2n}=\lim\limits\dfrac{\dfrac{5n}{n}+\dfrac{1}{n}}{\dfrac{2n}{n}}=\lim\limits\dfrac{5+\dfrac{1}{n}}{2}=\dfrac{5+0}{2}=\dfrac{5}{2}\)
b: \(\lim\limits\dfrac{6n^2+8n+1}{5n^2+3}\)
\(=\lim\limits\dfrac{\dfrac{6n^2}{n^2}+\dfrac{8n}{n^2}+\dfrac{1}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{3}{n^2}}\)
\(=\lim\limits\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}\)
\(=\dfrac{6+0+0}{5+0}=\dfrac{6}{5}\)
c: \(\lim\limits\dfrac{3^n+2^n}{4\cdot3^n}\)
\(=\lim\limits\dfrac{\dfrac{3^n}{3^n}+\left(\dfrac{2}{3}\right)^n}{4\cdot\left(\dfrac{3^n}{3^n}\right)}\)
\(=\lim\limits\dfrac{1+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1+0}{4}=\dfrac{1}{4}\)
d: \(\lim\limits\dfrac{\sqrt{n^2+5n+3}}{6n+2}\)
\(=\lim\limits\dfrac{\sqrt{\dfrac{n^2}{n^2}+\dfrac{5n}{n^2}+\dfrac{3}{n^2}}}{\dfrac{6n}{n}+\dfrac{2}{n}}\)
\(=\lim\limits\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}\)
\(=\dfrac{\sqrt{1+0+0}}{6}=\dfrac{1}{6}\)
\(a,lim\dfrac{5n+1}{2n}=lim\dfrac{\dfrac{5n}{n}+\dfrac{1}{n}}{\dfrac{2n}{n}}=lim\dfrac{5+\dfrac{1}{n}}{2}=\dfrac{5}{2}\\ b,lim\dfrac{6n^2+8n+1}{5n^2+3}=lim\dfrac{\dfrac{6n^2}{n^2}+\dfrac{8n}{n^2}+\dfrac{1}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{3}{n^2}}=lim\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}=\dfrac{6}{5}\)
\(c,lim\dfrac{3^n+2^n}{4.3^n}=\dfrac{\dfrac{3^n}{3^n}+\dfrac{2^n}{3^n}}{\dfrac{4.3^n}{3^n}}=\dfrac{1+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1}{4}\)
\(d,lim\dfrac{\sqrt{n^2+5n+3}}{6n+2}=lim\dfrac{\sqrt{\dfrac{n^2+5n+3}{n^2}}}{\dfrac{6n}{n}+\dfrac{2}{n}}=lim\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}=\dfrac{1}{6}\)

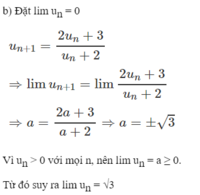
- Cách 1:
Đáp án C
- Cách 2 (phương pháp loại trừ): Từ các định lí ta thấy:
Các dãy ở phương án A,B đều bằng 0, do đó loại phương án A,B
Do đó loại phương án D. Chọn đáp án C