Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ảnh A’B’ của AB qua thấu kính phân kì luôn có độ cao nhỏ hơn vật.

Đáp án B
Đặt một vật sáng AB vuông góc với trục chính của thấu kính phân kì. Ảnh A’B’ của AB qua thấu kính có độ cao bao giờ cũng nhỏ hơn vật.

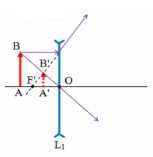
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{5}{h'}=\dfrac{40}{15}\Rightarrow h'=1,875cm\)
Tiêu cự thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{40}+\dfrac{1}{15}=\dfrac{11}{120}\)
\(\Rightarrow f=\dfrac{120}{11}cm\approx10,91cm\)

1.Vật AB được đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự 30cm. Nhìn qua thấu kính thấy ảnh A’B’ cao gấp hai lần AB. Khoảng cách từ vật đến kính là
60cm.
15cm.
30cm.
10cm.
2. Vật AB đặt cách thấu kính phân kì một khoảng 32cm cho ảnh A’B’ bằng AB/4. Khoảng cách từ A’B’ đến thấu kính là
12cm
8cm
16cm
18cm
3. Đặt vật sáng AB trước một thấu kính phân kì cho ảnh cao 0,8cm. Giữ nguyên vị trí vật thay thấu kính phân kì bằng một thấu kính hội tụ có cùng độ lớn tiêu cự và được đặt ở vị trí cũ của thấu kính phân kì thì thu được ảnh thật cao 4cm, khi đó khoảng cách giữa hai ảnh của vật trong hai trường hợp là 72cm. Tiêu cự của mỗi thấu kính và chiều cao của vật lần lượt là
f = 20cm, AB = 4cm.
f = 30cm, AB = 2cm.
f = 20cm, AB = 2cm.
f = 30cm, AB = 4cm.
4. Vật AB đặt trước một thấu kính O và vuông góc với trục chính của thấu kính, cho ảnh A’B’ cùng chiều và ở gần thấu kính hơn so với vật. Thông tin nào sau đây là sai ?
Ảnh A’B’ là ảnh ảo.
Thấu kính O là thấu kính hội tụ.
Ảnh A’B’ nhỏ hơn vật.
Thấu kính O là thấu kính phân kì.

Ta có: \(\Delta A'B'O'\sim\Delta ABO\Rightarrow\dfrac{A'B'}{AB}=\dfrac{O'A'}{OA}\left(1\right)\)
\(\Delta FA'B'\sim\Delta FOI\Rightarrow\dfrac{FA'}{OF}=\dfrac{A'B'}{OI}\left(2\right)\)
Và OI=AB, Từ (1) và (2) \(\Rightarrow\dfrac{OA'}{OA}=\dfrac{FA'}{OF}\left(3\right)\)
Mà FA'=OF-OA'
Hay \(\dfrac{OA'}{OA}=\dfrac{OF-OA'}{OF}\) thay số: \(\dfrac{OA'}{36}=\dfrac{18-OA'}{18}\Rightarrow OA'=12\left(cm\right)\)
Và: \(\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}\Rightarrow A'B'=\dfrac{AB.OA'}{OA}=\dfrac{4.12}{36}=1,33\left(cm\right)\)

b) Ảnh A'B' là ảnh ảo, cùng chiều và nhỏ hơn vật AB.
c) \(\Delta OAB~\Delta OA'B'\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Rightarrow\dfrac{30}{OA'}=\dfrac{5}{A'B'}\Rightarrow\dfrac{6}{OA'}=\dfrac{1}{A'B'}\) (1)
\(\Delta FOI~\Delta FA'B'\Rightarrow\dfrac{OF}{FA'}=\dfrac{OI}{A'B'}\Rightarrow\dfrac{15}{OF-OA'}=\dfrac{AB}{A'B'}\)\(\Rightarrow\dfrac{15}{15-OA'}=\dfrac{5}{A'B'}\Rightarrow\dfrac{3}{15-OA'}=\dfrac{1}{A'B'}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{6}{OA'}=\dfrac{3}{15-OA'}\Rightarrow\dfrac{2}{OA'}=\dfrac{1}{15-OA'}\Rightarrow30-2OA'=OA'\)\(\Rightarrow3OA'=30\Rightarrow OA'=10\left(cm\right)\)
\(\Rightarrow\dfrac{6}{10}=\dfrac{1}{A'B'}\Rightarrow A'B'=\dfrac{10}{6}\approx1,667\left(cm\right)\)
Vậy khoảng cách từ ảnh tới thấu kính là 10cm, chiều cao của ảnh là khoảng 1,667cm.

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{30}=\dfrac{1}{d'}-\dfrac{1}{20}\)
\(\Rightarrow d'=12cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{20}{12}\Rightarrow h'=1,8cm\)


Ảnh nhỏ hơn vật.