Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Giải thích: Đáp án A
+ Khi C = C1 , ta có: điện áp hiệu dụng giữa hai đầu tụ điện và hai đầu cuộn cảm có cùng giá trị và bằng U nên:
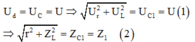
Điện áp toàn mạch khi đó:
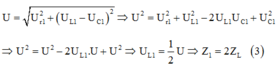
Thay vào (1), ta có: ![]()
Từ (2), (3), (4) ta có:
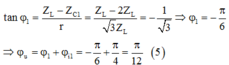
+ Khi C = C2 thì điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại nên
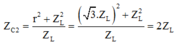
Tổng trở của mạch khi đó: ![]()
Độ lệch pha khi ZC = ZC2: 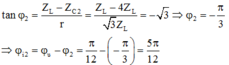
+ Áp dụng định luật Ôm cho cả hai trường hợp ta có:
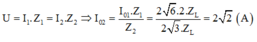
+ Biểu thức cường độ dòng điện khi ZC = ZC2:
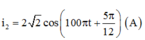

Đáp án B
+ Với φ 1 , φ 2 và φ 0 là độ lệch pha giữa u và I ứng với C 1 , C 2 , C 0
Ta có φ 1 + φ 2 = 2 φ 0 → φ 0 = - 52 , 5 0
+ Khi C C0 điện áp hiệu dụng trên tụ cực đại thì u R L vuông pha với u
+ Từ hình vẽ, ta có: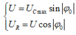
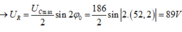
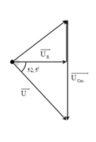

Đáp án B
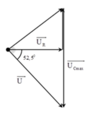
+ Với φ 1 , φ 2 v à φ 0 là độ lệch pha giữa u và i ứng với C 1 , C 2 , C 0 . Ta có
φ 1 + φ 2 = 2 φ 0
→ φ 0 = - 52 , 5 0
+ Khi C = C 0 điện áp hiệu dụng trên tụ cực đại thì u R L vuông pha với u.
+ Từ hình vẽ, ta có:
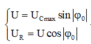
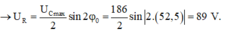

Tần số gíc của dòng điện:

- Dung kháng và cảm kháng của mạch điện:
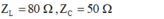
→ Dòng điện hiệu dụng trong mạch:
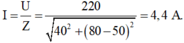

Đáp án A
L =
L
1
, i cùng pha u => cộng hưởng ![]()
L =
L
2
, Ul max 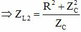
Để ý thấy
L
2
=
2
L
1
. Thay R = 50 vào, ta có hệ: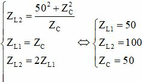
Từ đó dễ dàng tìm được f = 25(Hz).
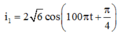
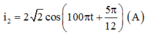
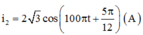
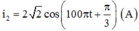
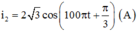

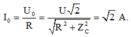
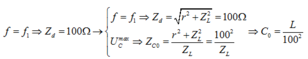
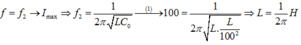
Chọn B
z c 1 = 1 ω C 1 = 30 Ω 1 max ⇔ z L = Z c 1 = 30 Ω U c m a x θ B c 2 = R 2 + Z L 2 Z L ⇒ 250 3 = R 2 + 30 2 30 ⇒ R = 40 Ω