Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Sử dụng tính chất dẫn điện của cuộn dây có điện trở thuần, lí thuyết về mạch điện xoay chiều chứa cuộn dây
Cách giải:
+ Khi đặt hiệu điện thế một chiều 15 V vào hai đầu cuộn dây ta có R = U 1 I 1 = 30 Ω
+ Khi đặt hiệu điện thế xoay chiều có giá trị hiệu dụng 15 V vào hai đầu cuộn dây ta có
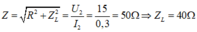

Chọn A.
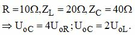
u L và u C ngược pha, có:
u L U o L = − u C U o C ⇔ 20 U o L = − u C U o C ⇒ u C = − 40 V
mạch R, L, C mắc nối tiếp nên
u = u R + u L + u C ⇔ 40 = u + R 20 − 40 ⇒ u R = 60 V
Do u R và u C vuông pha, có:
60 U o R 2 + − 40 4 U o R 2 = 1 ⇒ U o R = 10 37 V ⇒ I o = U o R R = 10 37 10 = 37 A ⇒ I = 37 2 ≈ 4 , 3 A .

Độ tự cảm L không có tác dụng gì với dòng một chiều.
Điện trở của cuộn dây: \(R=\frac{U}{I}=\frac{12}{0,15}=80\Omega\)
Đặt vào 2 đầu cuộn dây điện áp xoay chiều thì tổng trở \(Z=\sqrt{R^2+Z_L^2}=\frac{U}{I}=\frac{100}{1}=100\)
\(\Rightarrow\sqrt{80^2+Z_L^2}=100\)
\(\Rightarrow Z_L=60\Omega\)



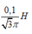
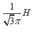
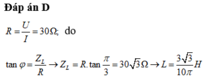
Điện trở cuộn dây là: \(R=20/1=20\Omega\)
Ta có: \(\cos\varphi=\dfrac{R}{Z}\)
\(\Rightarrow Z=\dfrac{20}{\cos\dfrac{\pi}{4}}=20\sqrt 2\Omega\)
Cường độ dòng điện hiệu dụng qua cuộn dây là: \(I=\dfrac{U}{Z}=\dfrac{20}{20\sqrt 2}=\dfrac{1}{\sqrt 2}(A)\)