Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài toán này bạn chỉ cần quan tâm đến phương án D là đúng thôi, vì để chứng minh B, C sai thì lại tương đối phức tạp, không cần thiết.
Theo giả thiết uC trễ pha pi/2 so vơi u --> u cùng pha với i --> Cộng hưởng, cường độ dòng điện đạt cực đại.
Vậy khi tăng f thì cường độ I giảm.
Chọn D.

Do giá trị hiệu dụng I1 = I2
nên Z1 = Z2
Ta có thể biểu diễn Z trên giản đồ như thế này.
i Z1 Z2 α α
Chiều của Z chính là chiều của điện áp u
+ So với i1 thì pha ban đầu của u là: \(\frac{\pi}{4}-\alpha\)
+ So với i2 thì pha ban đầu của u là: \(-\frac{\pi}{12}+\alpha\)
\(\Rightarrow\frac{\pi}{4}-\alpha=-\frac{\pi}{12}+\alpha\)
\(\Rightarrow\alpha=\frac{\pi}{6}\)
\(\Rightarrow\varphi_u=\frac{\pi}{4}-\frac{\pi}{6}=\frac{\pi}{12}\)
Vậy \(u=60\sqrt{2}\cos\left(100\pi t+\frac{\pi}{12}\right)V\)

Bài làm của em hoàn toàn đúng rồi, mình không thấy lỗi sai nào cả.

Ud Uc Um 120V 120V 45 45
Từ giản đồ véc tơ ta có: \(U_C=\sqrt{120^2+120^2}=120\sqrt{2}V\)
Cường độ dòng điện của mạch \(I=\frac{U_C}{Z_C}=\frac{120\sqrt{2}}{200}=0,6\sqrt{2}A\)
Công suất tiêu thụ cuộn dây: \(P=U.I\cos\varphi=120.0,6\sqrt{2}\cos45^0=72W\)


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

Uc U U U U U L r R MN AB A 50√3 50√3 30° M B N
Ta có giản đồ véc tơ như hình vẽ.
Tam giác AMB có BN vuông góc AM, MN vuông góc AB --> Suy ra AN vuông góc MB.
Tam giác AMB cân ở A, có AN là đường cao cũng là phân giác --> góc MAN = 300
--> Tam giác AMB đều
--> Ur = 1/3 trung tuyến = 1/3. 50√3 . √3/2 = 25V
--> Công suất tiêu thụ của cuộn dây: Pd = Ur.I = 25.2 = 50 W
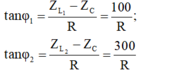
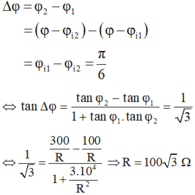
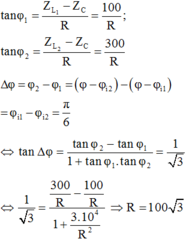
\(Z_C=100\Omega\)
\(Z_{L1}=200\Omega\)
\(Z_{L2}=400\Omega\)
Ta biểu diễn trên giản đồ véc tơ sự thay đổi của L như sau:
R Zc ZL2 ZL1 Z1 Z2 30 100 100 200 x O
Ta có: \(\tan30=\tan\left(Z_2OR-Z_1OR\right)=\frac{\tan Z_2OR-\tan Z_1OR}{1+\tan Z_2OR.\tan Z_1OR}\)
Suy ra: \(\frac{1}{\sqrt{3}}=\frac{\frac{300}{x}-\frac{100}{x}}{1+\frac{300}{x}.\frac{100}{x}}\)
Giải pt này em sẽ tìm đc x.