Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B.
Cường độ hiệu dụng chạy trong mạch
I = U Z = U R 2 + Z L − Z C 2 = max ⇔ Z L = Z C ⇔ ω = 1 L C ⇒ ω 2 L C = 1
Đáp án B
+ Cường độ dòng điện hiệu dụng trong mạch đạt giá trị cực đại khi xảy ra cộng hưởng ω 2 LC = 1
Đáp án A
Cách 1: Từ dấu hiệu “có hai giá trị ω 1 ≠ ω 2 thỏa P 1 = P 2 ; để I = I m a x thì ω = ? ”. Ta có:
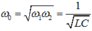
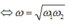
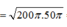
= 100 π r a d / s
Cách 2: Ta có:
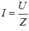
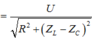
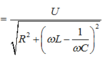
Để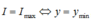 
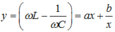
(Đặt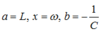
)
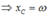
Từ dấu hiệu “hàm số: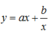 
, với hai giá trị
x
1
,
x
2
thì
y
1
=
y
2
”. Điều kiện để 
:
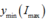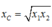
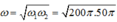
= 100 π r a d / s
Đáp án A.
Ta có:
Hay: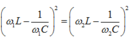 
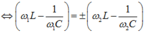
Vì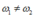 
nên
Khi có cộng hưởng 
thì 
hay: 
= 100 π r a d / s
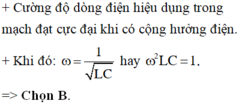
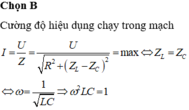
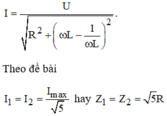
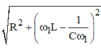
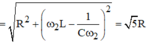
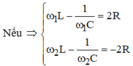
Chọn đáp án B
Cường độ dòng điện hiệu dụng trong mạch đạt cực đại khi có cộng hưởng điện.
Khi đó: ω = 1 L C hay ω 2 L C = 1