Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Ta có Um không đổi và để UAm luôn không đổ vs mọi gtri của R thì : Um=UAm hay ZL=2ZC =2.100=200 → L=2/π ( D)
Sử dụng hình vẽ suy luận cho nhanh : R ZL ZC UAm Um


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

\(Z_{C1}=\frac{1}{100\pi.\frac{10^{-4}}{4\pi}}=400\Omega\)
\(Z_{C2}=\frac{1}{100\pi.\frac{10^{-4}}{2\pi}}=200\Omega\)
Khi C thay đổi để P1 = P1 suy ra I1 = I2 => Z1 = Z2
\(\Rightarrow\sqrt{R^2+\left(Z_L-Z_{C1}\right)^2}=\sqrt{R^2+\left(Z_L-Z_{C2}\right)^2}\)
\(\Rightarrow Z_L-Z_{C1}=Z_{C2}-Z_L\)
\(\Rightarrow Z_L=\frac{Z_{C1}+Z_{C2}}{2}=300\Omega\)
\(\Rightarrow L=\frac{3}{\pi}\)
Đáp án C.

Đáp án C
ZL1 = 20 Ω, ZL2 = 80 Ω
![]()
i1 lệch pha 2π/3 so với i2 => i2 hợp với trục nằm ngang góc π/3
Ta có: 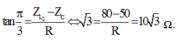


Đáp án C
L thay đổi, I bằng nhau nên ta có: Z L 1 − Z C = Z L 2 − Z C ⇒ Z C = Z L 1 + Z L 2 2 = 50 ( Ω )
Từ đó ta cũng rút ra được Z C − Z L 1 R = Z L 2 − Z C R ⇒ − tan φ 1 = tan φ 2 ⇒ φ 1 = − φ 2
Theo đề bài, φ 1 + φ 2 = 2 π 3 ⇒ φ 1 = − π 3 φ 2 = π 3 (vì ZL1 < ZL2 nên suy ra TH1 thì mạch có tính dung kháng, TH2 mạch có tính cảm kháng)
Có tan φ 2 = Z L 2 − Z C R ⇒ R = 10 3 ( Ω )