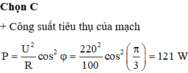Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Cường độ dòng điện cùng pha với điện áp -> \(Z_L=Z_C\)
Nếu nối tắt tụ C thì mạch chỉ còn R nối tiếp với L.
\(\tan\varphi=\frac{Z_L}{R}=\tan\frac{\pi}{3}=\sqrt{3}\Rightarrow Z_L=\sqrt{3}.50=50\sqrt{3}\Omega\)
\(\Rightarrow Z_C=50\sqrt{3}\Omega\)
2. Cuộn dây phải có điện trở R
Ta có giản đồ véc tơ
Ud Uc Um 120 120 Ur 45 0
Từ giản đồ ta có: \(U_C=\sqrt{120^2+120^2}=120\sqrt{2}V\)
\(U_R=120\cos45^0=60\sqrt{2}V\)
Cường độ dòng điện: \(I=\frac{U_C}{Z_C}=\frac{120\sqrt{2}}{200}=0,6\sqrt{2}V\)
Công suất: \(P=I^2R=I.U_R=0,6\sqrt{2}.60\sqrt{2}=72W\)

Đáp án C
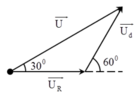
Phương pháp giản đồ vecto.
+ Từ hình vẽ, ta thấy rằng các vecto hợp thành một tam giác cân.
→ U = 2 U d cos 30 0 = 60 3 V

Chính là câu số 2 mình đã trả lời ở đây rùi bạn nhé: Hỏi đáp - Trao đổi kiến thức

Đáp án D

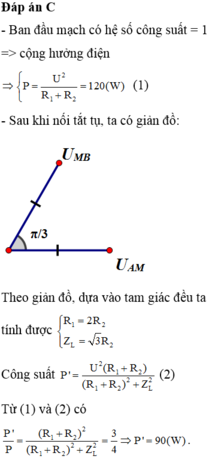
Lúc đầu P max = U 2 R 1 + R 2 = 160 W
Khi nối tắt hai đầu tụ thì: U A M = U M B , u A M lệch pha u M B góc 60 °
Dựa vào giản đồ véc-tơ ta có: φ = 30 °
Công suất tiêu thụ trên mạch AB lúc này là:
P = U 2 R 1 + R 2 cos 2 φ = 160 cos 2 30 ° = 120 W

Gọi r là điện trở cuộn dây. $U_d^2 = U_L^2 + U_r^2 \to U_L^2 + U_r^2 = {13^2}$ (1)
${U^2} = {\left( {{U_R} + {U_r}} \right)^2} + {\left( {{U_L} - {U_C}} \right)^2}$ → ${\left( {13 + {U_r}} \right)^2} + {\left( {{U_L} - 65} \right)^2} = {65^2}$(2)
Từ (1)(2) → ${U_r}$ = 12 V
Hệ số công suất của đoạn mạch là cosφ = $\dfrac{{{U_R} + {U_r}}}{U} = \dfrac{{13 + 12}}{{65}} = \dfrac{5}{{13}}$.

Đáp án A
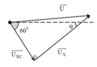
+ Tổng trở của mạch RC:
Z R C = U I = 160 Ω
+ Tổng trở của mạch RCX:
Z = U I = 200 Ω
Vì u R C vuông pha với
u X → Z X = Z 2 - Z R C 2 = 120 Ω → U X = 120 V .
Công suất tiêu thụ trên đoạn mạch X:
P = U I cos φ = 120 . 1 . cos 30 ° = 60 3 W