Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
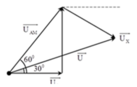
+ Biểu diễn vecto các điện áp (giả sử X có tính dung kháng).
+ Từ hình vẽ ta có U A M ¯ lệch pha so với U ¯ Áp dụng định lý hàm cos trong tam giác:

+ Dễ thấy rằng với các giá trị
![]()
→ U A M ¯ vuông pha với → U X ¯ từ đó ta tìm được X chậm pha hơn i một góc cos φ x = 3 2

Xét đoạn mạch MB có điện áp hiệu dụng gấp đôi điện áp hiệu dung trên R suy ra góc giữa \(U_{MB}\) và \(i\) là \(60^0\)
Mà \(u\) lệch pha \(90^0\) so với \(u_{MB}\)
Suy ra độ lệch pha giữa u và i là \(\varphi =30^0\)
Ta có:
\(P=U. I. \cos \varphi=120\sqrt 3.0,5.\cos30^0=90W\)


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

Điện áp giữ hai đầu đoạn mạch lệch pha \(\frac{\pi}{3}\) so với cường độ dòng điện:
\(\Rightarrow\cos\left(\frac{\pi}{3}\right)=\frac{R}{Z}\Leftrightarrow Z=80\Omega\)
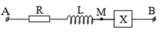

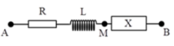
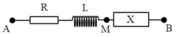


Giải thích: Đáp án A
Vì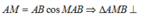 tại M
tại M
Cách 2. (Dùng máy tính cầm tay FX – 570VN
*Biễu diễn phức: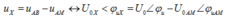
*Nhập máy :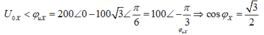
Chú ý: Công thức tính hệ số công suất không phụ thuộc vào cường độ I, vì vậy chúng ta có thể chuẩn hóa với giá trị I bất kì cho ra cùng kết quả.