Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bài ra ta có
u = U 0 cos(100 π t - π /3)
i = I 0 cos(100 π t - π /3 + π /2) = = I 0 sin(100 π t - π /3)
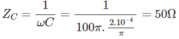
I 0 = U 0 / Z C = U 0 /50
Từ U 0 cos(100 π t - π /3) = 150
⇒ cos(100 π t - π /3) = 150/ U 0
I 0 sin(100 π t - π /3) = 4
⇒ sin(100 π t - π /3) = 200/ U 0
Từ
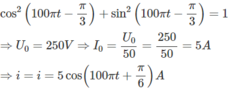

Độ lệch pha giữa u và i là: \(\varphi = \dfrac{\pi}{3}\)
Công suất tiêu thụ của đoạn mạch: \(P=U.I.\cos\varphi=100.1.\cos\dfrac{\pi}{3}=50W\)

Có \(I_0=\frac{U}{Z_C}\sqrt{2}=2\sqrt{2}\left(A\right)\)
Vì mạch chỉ có tụ điện $C$ nên cường độ dòng điện tức thời nhanh pha hơn điện áp tức thời một góc $\frac{\pi}{2}$
$\Rightarrow$ biểu thức: \(i=2\sqrt{2}\cos\left(100\pi t+\frac{\pi}{2}\right)\left(A\right)\), tức đáp án $A$ là đáp án đúng

Mạch chỉ gồm tụ điện và điện trở nên
\(U_C=U_{AB}.\sin\alpha=50\sqrt{3}V\)
đáp án A

Bạn nên gửi mỗi câu hỏi một bài thôi để mọi người tiện trao đổi.
1. \(Z_L=200\sqrt{3}\Omega\), \(Z_C=100\sqrt{3}\Omega\)
Suy ra biểu thức của i: \(i=1,1\sqrt{2}\cos\left(100\pi t-\frac{\pi}{3}\right)A\)
Công suất tức thời: p = u.i
Để điện áp sinh công dương thì p > 0, suy ra u và i cùng dấu.
Biểu diễn vị trí tương đối của u và i bằng véc tơ quay ta có:
u u i i 120° 120°
Như vậy, trong 1 chu kì, để u, i cùng dấu thì véc tơ u phải quét 2 góc như hình vẽ.
Tổng góc quét: 2.120 = 2400
Thời gian: \(t=\frac{240}{360}.T=\frac{2}{3}.\frac{2\pi}{100\pi}=\frac{1}{75}s\)
2. Khi nối tắt 2 đầu tụ điện thì cường độ dòng điện hiệu dụng không đổi \(\Rightarrow Z_1=Z_2\Leftrightarrow Z_C-Z_L=Z_L\Leftrightarrow Z_C=2Z_L\)
\(U_C=1,2U_d\Leftrightarrow Z_C=2Z_d\Leftrightarrow Z_C=2\sqrt{R^2+Z_L^2}\)
\(\Leftrightarrow2Z_L=\sqrt{R^2+Z_L^2}\Leftrightarrow R=\sqrt{3}Z_L\)
Khi bỏ tụ C thì cường độ dòng điện của mạch là: \(I=\frac{U}{Z_d}=\frac{U}{\sqrt{R^2+Z_L^2}}=\frac{220}{\sqrt{3.Z_L^2+Z_L^2}}=0,5\)
\(\Rightarrow Z_L=220\Omega\)

\(Z_C=\frac{1}{\omega C}=200\Omega\)
\(I_0=\frac{U_0}{Z_C}=\frac{100}{200}=0,5\)
Mạch điện chỉ có tụ C nên dòng điện sớm pha \(\frac{\pi}{2}\) so với u
\(\Rightarrow\varphi_i=\varphi_u+\frac{\pi}{2}=0\)
Vậy \(i=0,5\cos\left(100\pi t\right)\left(A\right)\)
B