Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng trở của mạch: \(Z=\frac{U}{I}=\frac{240}{\sqrt{3}}=80\sqrt{3}\left(\Omega\right)\)
\(Z_{MB}=\frac{80\sqrt{3}}{\sqrt{3}}=80\Omega\)
Ta có giản đồ véc tơ theo Z như sau:
i R Z Z Z r Z C AN L MB Z 80 80 80√3 80√2 45° 45° O
Từ giản đồ véc tơ ta có: \(Z_{AN}=80\sqrt{2}\)
Suy ra \(Z_C=80\)
Suy ra tam giác \(ORZ_{AN}\) vuông cân
\(\Rightarrow Z_LZ_{AN}Z_{MB}\) cũng vuông câ
\(\Rightarrow Z_L=80\cos45^0=40\sqrt{2}\)
Từ đó suy ra L

Dung kháng của tụ là \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \).

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
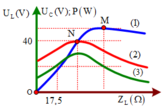
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)
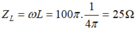
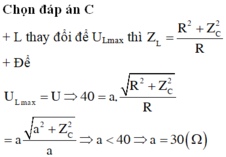
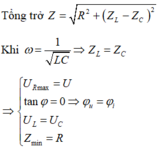


Đáp án B
Cảm kháng của cuộn dây là