Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(-1\le sin\left(x^2\right)\le1\Rightarrow\)\(0\le\sqrt{1-sin\left(x^2\right)}\le\sqrt{2}\Rightarrow-1\le y\le\sqrt{2}-1\)
\(y_{min}=-1\) khi \(sin\left(x^2\right)=1\Rightarrow x=\pm\sqrt{\dfrac{\pi}{2}+k2\pi}\) (\(k\in N\))
\(y_{max}=\sqrt{2}-1\) khi \(sin\left(x^2\right)=-1\Rightarrow x=\pm\sqrt{-\dfrac{\pi}{2}+k2\pi}\) (\(k\in Z^+\))

ĐKXĐ:
a. \(cos\left(x-\dfrac{2\pi}{3}\right)\ne0\Rightarrow x-\dfrac{2\pi}{3}\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{6}+k\pi\)
b. \(sin\left(x+\dfrac{\pi}{6}\right)\ne0\Rightarrow x+\dfrac{\pi}{6}\ne k\pi\Rightarrow x\ne-\dfrac{\pi}{6}+k\pi\)
c. \(\dfrac{1+x}{2-x}\ge0\Rightarrow-1\le x< 2\)

Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
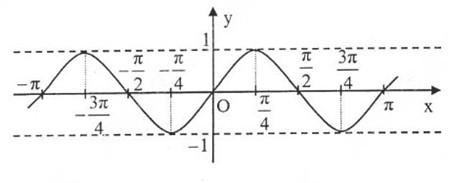
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)

Ta có y= 2sin2x +1.
Do - 1 ≤ sin 2 x ≤ 1 ⇒ - 2 ≤ 2 sin 2 x ≤ 2
⇒ - 1 ≤ 2 sin 2 x + 1 ≤ 3 ⇒ - 1 ≤ y ≤ 3
Vậy giá trị lớn nhất của hàm số bằng , giá trị nhỏ nhất bằng .
Chọn C.

\(y=1-cos2x+2sin2x+6=2sin2x-cos2x+7\)
\(y=\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sin2x-\dfrac{1}{\sqrt{5}}cos2x\right)+7\)
Đặt \(\dfrac{2}{\sqrt{5}}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\)
\(y=\sqrt{5}sin\left(2x-a\right)+7\)
\(\Rightarrow-\sqrt{5}+7\le y\le\sqrt{5}+7\)