Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)

1.
\(y'=\left(\dfrac{x}{lnx}\right)'.3^{\dfrac{x}{lnx}}.ln3=\dfrac{lnx-1}{ln^2x}.3^{\dfrac{x}{lnx}}.ln3\)
2.
\(y'=\left(tanx\right)'.tanx+\left(tanx\right)'.\dfrac{1}{tanx}=\dfrac{tanx}{cos^2x}+\dfrac{1}{tanx.cos^2x}\)
3.
\(y=\left(ln2x\right)^{\dfrac{2}{3}}\Rightarrow y'=\left(ln2x\right)'.\dfrac{2}{3}.\left(ln2x\right)^{-\dfrac{1}{3}}=\dfrac{1}{3x\sqrt[3]{ln2x}}\)

`a)TXĐ: R`
`b)TXĐ: R\\{0}`
`c)TXĐ: R\\{1}`
`d)TXĐ: (-oo;-1)uu(1;+oo)`
`e)TXĐ: (-oo;-1/2)uu(1/2;+oo)`
`f)TXĐ: (-oo;-\sqrt{2})uu(\sqrt{2};+oo)`
`h)TXĐ: (-oo;0) uu(2;+oo)`
`k)TXĐ: R\\{1/2}`
`l)ĐK: {(x^2-1 > 0),(x-2 > 0),(x-1 ne 0):}`
`<=>{([(x > 1),(x < -1):}),(x > 2),(x ne 1):}`
`<=>x > 2`
`=>TXĐ: (2;+oo)`
câu l) $x^2-1 > 0$ thì giải ra 2 nghiệm $x < -1, x > 1$ mới đúng chứ nhỉ?

a: \(y=\left(2x^2-x+1\right)^{\dfrac{1}{3}}\)
=>\(y'=\dfrac{1}{3}\left(2x^2-x+1\right)^{\dfrac{1}{3}-1}\cdot\left(2x^2-x+1\right)'\)
\(=\dfrac{1}{3}\cdot\left(4x-1\right)\left(2x^2-x+1\right)^{-\dfrac{2}{3}}\)
b: \(y=\left(3x+1\right)^{\Omega}\)
=>\(y'=\Omega\cdot\left(3x+1\right)'\cdot\left(3x+1\right)^{\Omega-1}\)
=>\(y'=3\Omega\left(3x+1\right)^{\Omega-1}\)
c: \(y=\sqrt[3]{\dfrac{1}{x-1}}\)
=>\(y'=\dfrac{\left(\dfrac{1}{x-1}\right)'}{3\cdot\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}\)
\(=\dfrac{\dfrac{1'\left(x-1\right)-\left(x-1\right)'\cdot1}{\left(x-1\right)^2}}{\dfrac{3}{\sqrt[3]{\left(x-1\right)^2}}}\)
\(=\dfrac{-x}{\left(x-1\right)^2}\cdot\dfrac{\sqrt[3]{\left(x-1\right)^2}}{3}\)
\(=\dfrac{-x}{\sqrt[3]{\left(x-1\right)^4}\cdot3}\)
d: \(y=log_3\left(\dfrac{x+1}{x-1}\right)\)
\(\Leftrightarrow y'=\dfrac{\left(\dfrac{x+1}{x-1}\right)'}{\dfrac{x+1}{x-1}\cdot ln3}\)
\(\Leftrightarrow y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}:\dfrac{ln3\left(x+1\right)}{x-1}\)
\(\Leftrightarrow y'=\dfrac{x-1-x-1}{\left(x-1\right)^2}\cdot\dfrac{x-1}{ln3\cdot\left(x+1\right)}\)
\(\Leftrightarrow y'=\dfrac{-2}{\left(x-1\right)\cdot\left(x+1\right)\cdot ln3}\)
e: \(y=3^{x^2}\)
=>\(y'=\left(x^2\right)'\cdot ln3\cdot3^{x^2}=2x\cdot ln3\cdot3^{x^2}\)
f: \(y=\left(\dfrac{1}{2}\right)^{x^2-1}\)
=>\(y'=\left(x^2-1\right)'\cdot ln\left(\dfrac{1}{2}\right)\cdot\left(\dfrac{1}{2}\right)^{x^2-1}=2x\cdot ln\left(\dfrac{1}{2}\right)\cdot\left(\dfrac{1}{2}\right)^{x^2-1}\)
h: \(y=\left(x+1\right)\cdot e^{cosx}\)
=>\(y'=\left(x+1\right)'\cdot e^{cosx}+\left(x+1\right)\cdot\left(e^{cosx}\right)'\)
=>\(y'=e^{cosx}+\left(x+1\right)\cdot\left(cosx\right)'\cdot e^u\)
\(=e^{cosx}+\left(x+1\right)\cdot\left(-sinx\right)\cdot e^u\)
a) \(y=\left(2x^2-x+1\right)^{\dfrac{1}{3}}\)
\(\Rightarrow y'=\dfrac{1}{3}.\left(2x^2-x+1\right)^{\dfrac{1}{3}-1}.\left(4x-1\right)\)
\(\Rightarrow y'=\dfrac{1}{3}.\left(2x^2-x+1\right)^{-\dfrac{2}{3}}.\left(4x-1\right)\)
b) \(y=\left(3x+1\right)^{\pi}\)
\(\Rightarrow y'=\pi.\left(3x+1\right)^{\pi-1}.3=3\pi.\left(3x+1\right)^{\pi-1}\)
c) \(y=\sqrt[3]{\dfrac{1}{x-1}}\)
\(\Rightarrow y'=\dfrac{\left(x-1\right)^{-1-1}}{3\sqrt[3]{\left(\dfrac{1}{x-1}\right)^{3-1}}}=\dfrac{\left(x-1\right)^{-2}}{3\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}=\dfrac{1}{3.\sqrt[]{x-1}.\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}\)
\(\Rightarrow y'=\dfrac{1}{3\left(x-1\right)^{\dfrac{1}{2}}.\left(x-1\right)^{\dfrac{2}{3}}}=\dfrac{1}{3\left(x-1\right)^{\dfrac{7}{6}}}=\dfrac{1}{3\sqrt[6]{\left(x-1\right)^7}}\)
d) \(y=\log_3\left(\dfrac{x+1}{x-1}\right)\)
\(\Rightarrow y'=\dfrac{\dfrac{1-\left(-1\right)}{\left(x-1\right)^2}}{\dfrac{x+1}{x-1}.\ln3}=\dfrac{2}{\left(x+1\right)\left(x-1\right).\ln3}\)
e) \(y=3^{x^2}\)
\(\Rightarrow y'=3^{x^2}.ln3.2x=2x.3^{x^2}.ln3\)
f) \(y=\left(\dfrac{1}{2}\right)^{x^2-1}\)
\(\Rightarrow y'=\left(\dfrac{1}{2}\right)^{x^2-1}.ln\dfrac{1}{2}.2x=2x.\left(\dfrac{1}{2}\right)^{x^2-1}.ln\dfrac{1}{2}\)
Các bài còn lại bạn tự làm nhé!

d: ĐKXĐ: \(x^2-1< >0\)
=>\(x^2\ne1\)
=>\(x\notin\left\{1;-1\right\}\)
Vậy: TXĐ là D=R\{1;-1}
b: ĐKXĐ: \(2-x^2>0\)
=>\(x^2< 2\)
=>\(-\sqrt{2}< x< \sqrt{2}\)
Vậy: TXĐ là \(D=\left(-\sqrt{2};\sqrt{2}\right)\)
a: ĐKXĐ: \(x-1>0\)
=>x>1
Vậy: TXĐ là \(D=\left(1;+\infty\right)\)
c: ĐKXĐ: \(x^2+x-6>0\)
=>\(x^2+3x-2x-6>0\)
=>\(\left(x+3\right)\left(x-2\right)>0\)
TH1: \(\left\{{}\begin{matrix}x+3>0\\x-2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>2\\x>-3\end{matrix}\right.\)
=>x>2
TH2: \(\left\{{}\begin{matrix}x+3< 0\\x-2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< -3\\x< 2\end{matrix}\right.\)
=>x<-3
Vậy: TXĐ là \(D=\left(2;+\infty\right)\cup\left(-\infty;-3\right)\)
e: ĐKXĐ: \(x^2-2>0\)
=>\(x^2>2\)
=>\(\left[{}\begin{matrix}x>\sqrt{2}\\x< -\sqrt{2}\end{matrix}\right.\)
Vậy: TXĐ là \(D=\left(-\infty;-\sqrt{2}\right)\cup\left(\sqrt{2};+\infty\right)\)
f: ĐKXĐ: \(\sqrt{x-1}>0\)
=>x-1>0
=>x>1
Vậy: TXĐ là \(D=\left(1;+\infty\right)\)
g: ĐKXĐ: \(x^2+x-6>0\)
=>\(\left(x+3\right)\left(x-2\right)>0\)
=>\(\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\)
Vậy: TXĐ là \(D=\left(2;+\infty\right)\cup\left(-\infty;-3\right)\)

Đáp án: A.
Nhận xét rằng hàm số dạng 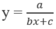 (a, b
≠
0) có tiệm cận đứng là
(a, b
≠
0) có tiệm cận đứng là 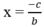 và tiệm cận ngang là y = 0.
và tiệm cận ngang là y = 0.

\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
đơn điệu trên R là sao bạn? bạn chỉ mk cách nhận bt đc ko?

Đáp án: A.
Nhận xét rằng hàm số dạng 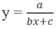 (a, b ≠ 0) có tiệm cận đứng là
(a, b ≠ 0) có tiệm cận đứng là 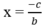 và tiệm cận ngang là y = 0.
và tiệm cận ngang là y = 0.

\(\left(\frac{2x-1}{x+2}\right)'=\frac{5}{\left(x+2\right)^2}>0\)
Vậy hàm số \(y=\frac{2x-1}{x+2}\) đồng biến trên R. Chọn A.
A. là hàm phân thức bậc nhất trên bậc nhất nên không đồng biến trên \(ℝ\).
B., D. là đa thức, có hệ số cao nhất âm nên cũng không thể đồng biến trên \(ℝ\).
C>: \(\left(x^3+2x+1\right)'=3x^2+2>0,\forall x\inℝ\).
Ta chọn C.
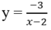
Chọn D.
Ta có: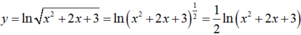
Do đó: