Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. TXĐ: D=R
$y'=3x^2-6x=0\Leftrightarrow x=0$ hoặc $x=2$
$y''=6x-6$
$y''(0)=-6<0$ nên hàm số đạt cực đại tại $x=0$, giá trị cực đại tương ứng là $y=9$
$y''(2)=6>0$ nên hàm số đạt cực tiểu tại $x=2$, giá trị cực tiểu tương ứng là $y=5$
b. TXĐ: $D=R$
$y=\frac{1}{3}x^3-2x^2+15x+3$
$y'=x^2-4x+15=(x-2)^2+11>0$ với mọi $x\in D$
Do đó hàm $y$ đồng biến trên toàn tập xác định nên không có cực trị.

a.
\(y'=-\dfrac{3}{2}x^3+\dfrac{6}{5}x^2-x+5\)
b.
\(y'=\dfrac{\left(x^2+4x+5\right)'}{2\sqrt{x^2+4x+5}}=\dfrac{2x+4}{2\sqrt{x^2+4x+5}}=\dfrac{x+2}{\sqrt{x^2+4x+5}}\)
c.
\(y=\left(3x-2\right)^{\dfrac{1}{3}}\Rightarrow y'=\dfrac{1}{3}\left(3x-2\right)^{-\dfrac{2}{3}}=\dfrac{1}{3\sqrt[3]{\left(3x-2\right)^2}}\)
d.
\(y'=2\sqrt{x+2}+\dfrac{2x-1}{2\sqrt{x+2}}=\dfrac{6x+7}{2\sqrt{x+2}}\)
e.
\(y'=3sin^2\left(\dfrac{\pi}{3}-5x\right).\left[sin\left(\dfrac{\pi}{3}-5x\right)\right]'=-15sin^2\left(\dfrac{\pi}{3}-5x\right).cos\left(\dfrac{\pi}{3}-5x\right)\)
g.
\(y'=4cot^3\left(\dfrac{\pi}{6}-3x\right)\left[cot\left(\dfrac{\pi}{3}-3x\right)\right]'=12cot^3\left(\dfrac{\pi}{6}-3x\right).\dfrac{1}{sin^2\left(\dfrac{\pi}{3}-3x\right)}\)

a.
\(y'=\dfrac{\left(1+\sqrt{3x-1}\right)'}{1+\sqrt{3x-1}}=\dfrac{3}{2\left(1+\sqrt{3x-1}\right)\sqrt{3x-1}}\)
b.
\(y'=\dfrac{\left(2sin^2x-1\right)'}{\left(2sin^2x-1\right).ln10}=\dfrac{2sin2x}{\left(2sin^2x-1\right)ln10}\)
c.
\(y'=\left(3x^2+3\right)3^{x^3+3x+1}.e^x.ln3+3^{x^3+3x+1}.e^x\)

Đáp án: D.
Tiệm cận đứng của đồ thị hàm số 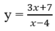 là x = 4; tiệm cận ngang của đồ thị hàm số đó là y = 3. Diện tích hình chữ nhật tạo thành là 3 x 4 = 12.
là x = 4; tiệm cận ngang của đồ thị hàm số đó là y = 3. Diện tích hình chữ nhật tạo thành là 3 x 4 = 12.

Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 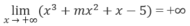
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.
Chọn B