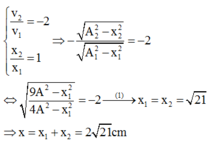Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Tại thời điểm t 1 thì:
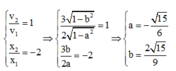
Dễ thấy a và b trái dấu, để đơn giản chọn a < 0 => b > 0
Ta có:
![]()
Tại thời điểm t 2
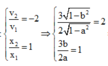
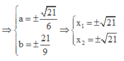

Đáp án A
Đặt a = cos(ωt + φ1) và b = cos(ωt + φ2)
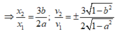
Tại thời điểm t1 thì:
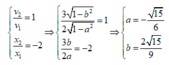
Dễ thấy a và b trái dấu,
để đơn giản chọn a < 0 => b > 0.
Ta có: x = x1 + x2 = A(2a + 3b)
= -2Aa = 15 => A = 3 cm
Tại thời điểm t2 thì: 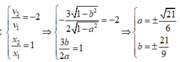
Nhận thấy trường hợp này a, b cùng dấu. Dựa vào 4 đáp án => lấy a > 0, b > 0.
Vậy khi đó ta có li độ dao động tổng hợp:
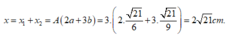

Hướng dẫn bạn:
- Lực kéo về: \(F=k.x=0,03\sqrt 2\pi\) (không biết có đúng như giả thiết của bạn không)
\(\Rightarrow x =\dfrac{0,03\sqrt 2\pi}{k}=\dfrac{0,03\sqrt 2\pi}{m.\omega^2}=\dfrac{0,03\sqrt 2\pi}{0,01.\omega^2}=\dfrac{3\sqrt 2\pi}{\omega^2}\)
- Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 0,05^2=(\dfrac{3\sqrt 2\pi}{\omega^2})^2+\dfrac{(0,4\pi)^2}{\omega^2}\)
Bạn giải pt trên tìm \(\omega \) và suy ra chu kì \(T\) nhé.

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

1. B là chu kỳ của dao động.
2. C. Quỹ đạo là đoạn thằng.
3. D. Lực kéo về tỉ lệ với li độ và luôn hướng về vị trí cân bằng. \(\left|F\right|=k\left|x\right|\)
4. Đáp án C sai.
Câu này bạn có thể nhớ giản đồ véc tơ này

Khi đó v sớm pha hơn li độ x 1 góc pi/2
a sớm pha hơn v 1 góc là pi/2
còn a sớm pha hơn x 1 góc pi/2

 chọn A
chọn A
Giải thích: Đáp án D
Phương pháp: Sử dụng hê ̣thức độc lập theo thời gian của x và v
Cách giải:
- Tại thời điểm t:
- Tại thời điểm t + ∆t: