Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
\(A=1-\frac{1}{1+2}+\frac{1}{2+3}+\frac{1}{3+4}+...+\frac{1}{18+19}+\frac{1}{19+20}\)
\(A=1-\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{18}-\frac{1}{19}+\frac{1}{19}-\frac{1}{20}\)
\(A=1-1-\frac{1}{20}\)
\(A=0-\frac{1}{20}\)
\(A=-\frac{1}{20}\)
\(A=-0,05\)
=> A không phải là số nguyên ( đpcm )
# Chúc bạn học tốt #

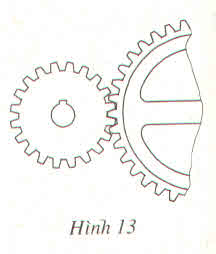
Vì số răng cưa và vận tốc là hai đại lượng tỉ lệ nghịch với nhau nên ta có:
x20=60yx20=60y hay xy = 60.20
Nên y=1200x
Vì số thời gian không đổi nên số răng cưa và số vòng quay là 2 đại lượng tỉ lệ nghịch.
\(\Rightarrow\dfrac{20}{y}=\dfrac{x}{60}\\ \Leftrightarrow xy=20.60\\ \Rightarrow xy=1200\\ \Rightarrow y=\dfrac{1200}{x}\)
Vậy \(y=\dfrac{1200}{x}\)

\(\frac{8^{11}.3^{17}}{27^{10}.9^{15}}=\frac{8^{11}.3^{17}}{3^{30}.3^{30}}=\frac{8^{11}}{3^{13}.3^{30}}=\frac{8^{11}}{3^{43}}\)
\(\frac{\left(5^4-5^3\right)^3}{125^4}=\frac{[\left(5-1\right).5^3]^3}{5^{12}}=\frac{\left(4.5^3\right)^3}{5^{12}}=\frac{64.5^9}{5^{12}}=\frac{64}{5^3}=\left(\frac{4}{5}\right)^3\)
\(\frac{4^{20}-2^{20}+6^{20}}{6^{20}-3^{20}+9^{20}}=\frac{2^{40}-2^{20}+6^{20}}{6^{20}-3^{20}+3^{40}}=\frac{2^{20}.\left(2^{20}-1+3^{30}\right)}{3^{20}.\left(2^{20}-2+3^{20}\right)}=\frac{2^{20}}{3^{20}}=\left(\frac{2}{3}\right)^{20}\)
Nếu A là trung điểm của đoạn BC
=> \(BA=AC=\frac{BC}{2}\)
Theo đề bài ta có:
\(AM_1=\frac{2^{2001}}{2}=2^{2000}\)
\(AM_2=\frac{2^{2000}}{2}=2^{1999}\)
\(AM_3=\frac{2^{1999}}{2}=2^{1998}\)
...................
\(AM_{2010}=\frac{2^{-8}}{2}=2^{-9}\)
\(AM_{2011}=\frac{2^{-9}}{2}=2^{-10}\)
Vậy độ dài đoạn thẳng \(AM_{2010};AM_{2011}\) lần lượt có số đo là: \(2^{-9};2^{-10}\)
Bài này các bạn đổi \(2^{-9};2^{-10}\) về phân số cũng được nhé , tiếc =="
, tiếc =="
Do lấy điểm chuẩn là 17 điểm nên thêm 4 bạn sau cũng được vào vòng trong:
31. Nguyễn Hữu Thế
32. Nguyên Thị Thu trang
33. Trần Hương Thoan
34. BAN is VBN