Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tìm diện tích của một hình thang , biết rằng khi kéo dài đáy nhỏ về hai phía để được hình vuông có cạnh là đáy lớn của hình thang thì dduocj diện tích của hình mới là 81 c
Vì các hình thang vuông PQMA, QMBC, QPNC, PNDA bằng nhau nên:
MQ = NP = QP = 4cm và CN = AD.
Mặt khác AD = NP + QM = 4+4 = 8 (cm)
Do đó : CN = AD = 8cm.
Diện tích hình thang vuông PQCN là : (CN + PQ) x NP : 2 = (8+4) x 4 : 2 = 24 (cm2)
Suy ra diện tích hinh chữ nhật ABCD là: 24 x 4 = 96 (cm2)
Ta có:(x+1)+(x+4)+(x+7)+...+(x+28)=155
=> x+1+x+4+x+7+...+x+28= 15
=> x+x+x+...+x+1+4+7+...+28=155
Từ 1 đến 28 có:(28-1):3+1=10
=> x.10+(1+28).10:2=155
=> x.10+29.5=155
=> x.10+145=155
=> x.10=10
=> x=1
Vậy x=1
Có số chữ số x là:
(28-1):3+1=10(số)
Tổng các số mà x cộng vào là:
(8+1)x10:2=145
Ta có:
Xx10+145=155
Xx10=155-145
Xx10=140
X=140:10
X=14
* Xét trường hợp tất cả các chữ số a, b, c, d, e đều lớn hơn hoặc bằng 1, khi đó mẫu số:
=>
=> Vế trái lớn hơn a và nhỏ hơn a + 1
=> a < 225/157 < a + 1
Mà 225/157 = 1 + 68/157 => a = 1.
Suy ra
Tương tự lý luận như trên suy ra b = 2; c = 3; d = 4; e = 5. Tích a.b.c.d.e = 1.2.3.4.5 = 120
* Trường hợp một trong các chữ số a, b, c, d, e bằng 0, không cần phải kiểm tra thỏa mãn đẳng thức đã cho, ta thấy tích a.b.c.d.e = 0 (nhỏ thua 120)
Vậy tích a.b.c.d.e lớn nhất là bằng 120 khi a = 1, b = 2, c = 3, d = 4, e= 5
.png)
.png)
.png)
Hình a:
Đáy là AB
Đường cao là CH
Hình b:
Đáy là EG
Đường cao là DK
Hình c:
Đáy là PQ
Đường cao là MN
Độ dài đáy BC của tam giác ABC là:
200 x 2 : 25 = 16 ( cm )
Đ/S: 16 cm
độ dài đáy BC của tam giác ABC là
\(\left(200\times2\right)\div25=16\left(cm\right)\)
đáp số : \(16cm\)
Bài giải
Vì bốn điểm M , N , P , Q là trung điểm các cạnh AB, BC, CD, DA nên diện tích hình tứ giác MNPQ bằng \(\frac{1}{2}\) diện tích hình thang ABCD.
Diện tích hình thang ABCD là :
115 : \(\frac{1}{2}\) = 230 ( cm2 )
Đáp số : 230 cm2
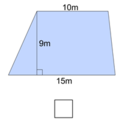
Diện tích hình thang bên trái:
(10 + 15) x 9 : 2 = 112,5 (m2) > 100m2
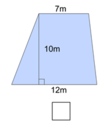
Diện tích hình thang bên phải:
(7 + 12) x 10 : 2 = 95 (m2) < 100m2
Vậy đánh dấu (x) vào ô trống ở hình thang bên trái: