Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
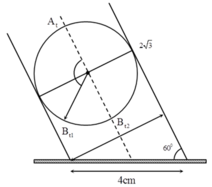
+ Khi A đi từ vị trí cao nhất đến thấp nhất thì mất khoảng thời gian là:
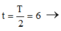 T = 12 s.
T = 12 s.
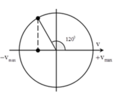
+ Trong khoảng t = 2 s thì B đi từ Bt1 đến Bt2 như hình vẽ:
![]() B nhanh pha hơn A một góc
B nhanh pha hơn A một góc
+ Từ hình vẽ ta có thể tìm được biên độ dao động của cái bóng là: A = 4 cm.
+ Khi A có vận tốc cực đại (tại vị trí At là VTCB) thì khi đó B đang ở Bt1.
![]()
Và vì B đang đi về VTCB nên v đang tăng

Tại thời điểm t = 3T/4 nên ta có:
![]()
a = - ω 2 Acos2 π = - 10 π 2 .0,2.1 = -197 ≈ -200 m/ s 2
Ta thấy vecto a → hướng theo chiều âm của trục x về vị trí cân bằng
F = ma = 0,050.(-197) = -9,85 ≈ -9,9N < 0
Vecto F → cùng hướng cùng chiều với vecto a →

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

Giải thích: Đáp án D
Phương pháp: Phương trình của x, v, a:
Cách giải:
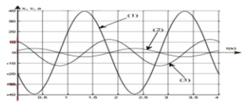
Từ đồ thị ta thấy: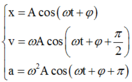
(1) sớm pha hơn (3) góc π/2
(3) sớm pha hơn (2) góc π/2
=> (2) là đồ thị của x(t); (3) là đồ thị của v(t); (1) là đồ thị của a(t)

Sau khoảng thời gian \(\Delta t\) thanh kim loại quét được một diện tích \(S=l\cdot v\cdot\Delta t\).
Từ thông qua dây dẫn:
\(\Delta\Phi=BS\cdot cos\alpha\)
Theo bài phương đường sức từ và phương của vecto vận tốc thanh luôn vuông góc với nhau.
\(\Rightarrow\alpha=90^o\)
\(\Rightarrow\Delta\Phi=B\cdot lv\Delta t\)
\(\Rightarrow v=\dfrac{\Delta\Phi}{B\cdot l\Delta t}=\dfrac{1}{1\cdot0,1}=10\)m/s
TK
Sau khoảng thời gian ΔtΔt thanh kim loại quét được một diện tích S=l⋅v⋅ΔtS=l⋅v⋅Δt.
Từ thông qua dây dẫn:
ΔΦ=BS⋅cosαΔΦ=BS⋅cosα
Theo bài phương đường sức từ và phương của vecto vận tốc thanh luôn vuông góc với nhau.
⇒α=90o⇒α=90o
⇒ΔΦ=B⋅lvΔt⇒ΔΦ=B⋅lvΔt
⇒v=ΔΦB⋅lΔt=11⋅0,1=10⇒v=ΔΦB⋅lΔt=11⋅0,1=10m/s

Đáp án A
+ Tần số góc của dao động: ω = k m = 60 150.10 − 3 = 20 rad/s
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 150.10 − 3 .10 60 = 2 , 5 c m
+ Biên độ dao động ban đầu của vật: A = Δ l 0 2 + v 0 ω 2 = 2 , 5 2 + 50 3 20 2 = 5 cm.
Điện trường xuất hiện, vật đang ở vị trí động năng bằng ba lần thế năng, tại vị trí này vật có x = 0,5A = 2,5 cm, v = 3 2 ω A = 50 3 cm/s.
+ Dưới tác dung của điện trường con lắc sẽ dao động điều hòa tại vị trí cân bằng mới O′ nằm dưới vị trí cân bằng cũ một đoạn Δ l = q E k = 6.10 − 5 .2.10 4 60 = 2 cm.
→ So với vị trí cân bằng mới, tại vị thời điểm xảy ra biến cố, vật có x′ = 2,5 – 2 = 0,5 cm, v ' = 3 2 ω A = 50 3 cm/s.
Biên độ dao động mới: A ' = x ' 2 + v ' ω 2 ⇒ 0 , 5 2 + 50 3 20 2 = 19 cm.

Từ đồ thị ta thấy:
(1) sớm pha hơn (3) góc π/2
(3) sớm pha hơn (2) góc π/2
=> (2) là đồ thị của x(t); (3) là đồ thị của v(t); (1) là đồ thị của a(t)
Đáp án D
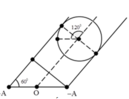


a)Vị trí ban đầu quả bóng là điểm phát bóng nằm ở cuối ngọn đồi. Vecto vị trí là: \(\overrightarrow{r_0}=0i+0j\)
Vecto vị trí quả bóng tại thời điểm t là: \(\overrightarrow{r}=18ti+\left(4t-4\cdot9t^2\right)j\)
b)Hàm vecto vận tốc của bóng theo thời gian:
\(\overrightarrow{v}=\left(\overrightarrow{r}\right)'=18i+\left(4-4\cdot9\cdot2t\right)j=18i+\left(4-4\cdot18t\right)j\)
c)Vecto gia tốc theo thời gian:
\(\overrightarrow{a}=\left(\overrightarrow{v}\right)'=0i+\left(-4\cdot18\right)j=-4\cdot18j\)
d)Tại \(t=3s\):
Vị trí: \(\overrightarrow{r}=18\cdot3i+\left(4\cdot3-4\cdot9\cdot3^2\right)j=54i-312j\left(m\right)\)
Vận tốc: \(\overrightarrow{v}=18i-212j\left(m/s\right)\)
Gia tốc: \(\overrightarrow{a}=-4\cdot18j\left(m/s^2\right)\)