TM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
B
1
HQ
Hà Quang Minh
Giáo viên
10 tháng 1 2024
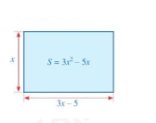
\(3{{\rm{x}}^2} - 5{\rm{x = x}}\left( {3{\rm{x}} - 5} \right)\)
HQ
Hà Quang Minh
Giáo viên
13 tháng 1 2024
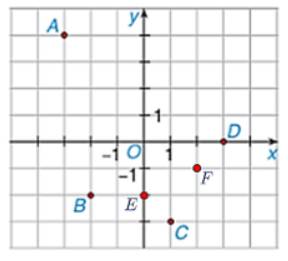
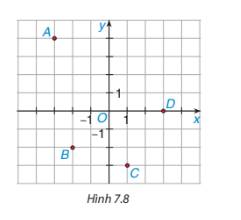
a) Có A(–3; 4), B(–2; –2), C(1; –3), D(3; 0).
b) Ta có các điểm E(0; –2) và F(2; –1) được biểu diễn như sau:
NT
3
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Vì hai hình đồng dạng phối cảnh \(H\) và \({H_1}\) có tỉ số đồng dạng \(k = \frac{2}{3}\) nên \(\frac{{3,6}}{x} = \frac{2}{y} = \frac{2}{3} \Rightarrow \left\{ \begin{array}{l}\frac{{3,6}}{x} = \frac{2}{3}\\\frac{2}{y} = \frac{2}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 5,4\\y = 3\end{array} \right.\)
Vậy \(x = 5,4cm;y = 3cm\).
b) Hình \({H_1}\) và hình \(H'\) là hai hình bằng nhau vì chúng có kích thước bằng nhau và khi ta đặt hình \({H_1}\) nằm ngang sẽ thu được hình \(H'\).
B
1
HQ
Hà Quang Minh
Giáo viên
13 tháng 1 2024
Đáp án đúng là: C
Trong Hình 4.31 có \(\widehat {AMN} = \widehat {ABC}\) mà hai góc này ở vị trí đồng vị nên MN // BC.
Áp dụng định lí Thalès vào tam giác ABC, ta có:
\(\dfrac{{AM}}{{BM}} = \dfrac{{AN}}{{CN}}\) hay \(\dfrac{2}{3} = \dfrac{{1,5}}{x}\)
Suy ra \(x = \dfrac{{1,5.3}}{2} = 2,25\)
Vậy x = 2,25.
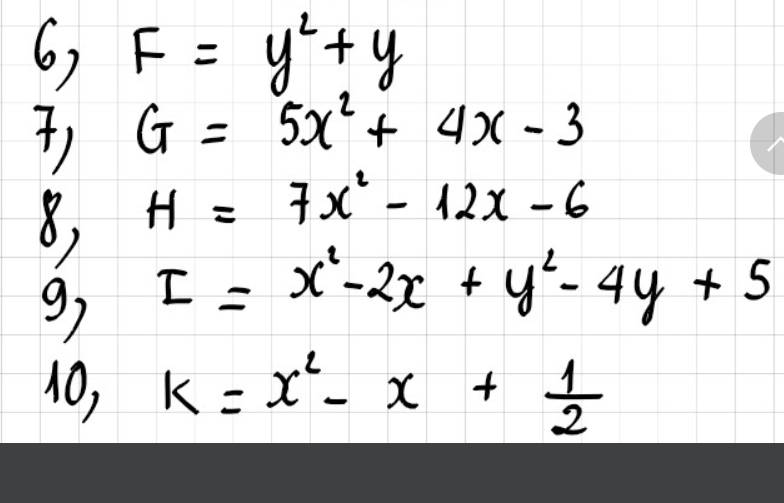
6:
=y^2+y+1/4-1/4
=(y+1/2)^2-1/4>=-1/4
Dấu = xảy ra khi y=-1/2
7:
=5(x^2+4/5x-3/5)
=5(x^2+2*x*2/5+4/25-19/25)
=5(x+2/5)^2-19/5>=-19/5
Dấu = xảy ra khi x=-2/5
8: =7(x^2-12/7x-6/7)
=7(x^2-2*x*6/7+36/49-78/49)
=7*(x-6/7)^2-78/7>=-78/7
Dấu = xảy ra khi x=6/7
9: =x^2-2x+1+y^2-4y+4
=(x-1)^2+(y-2)^2>=0
Dấu = xảy ra khi x=1 và y=2
10: =x^2-x+1/4+1/4
=(x-1/2)^2+1/4>=1/4
Dấu = xảy ra khi x=1/2