Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x,y\in Z\Rightarrow\left\{{}\begin{matrix}x-1,3-y\in Z\\x-1,3-y\inƯ\left(-7\right)=\left\{\pm1;\pm7\right\}\end{matrix}\right.\)
Ta có bảng:
| x-1 | -1 | 1 | -7 | 7 |
| 3-y | 7 | -7 | 1 | -1 |
| x | 0 | 2 | -6 | 8 |
| y | -4 | 10 | 2 | 4 |
Vậy \(\left(x,y\right)\in\left\{\left(0;-4\right);\left(2;10\right);\left(-6;2\right);\left(8;4\right)\right\}\)

\(M=\dfrac{3x\left(x-3\right)+2}{x-3}\)
\(\Rightarrow M=\dfrac{3x\left(x-3\right)}{x-3}+\dfrac{2}{x-3}\)
\(\Rightarrow M=3x+\dfrac{2}{x-3}\)
Để M nguyên thì \(\dfrac{2}{x-3}\in Z\Rightarrow x-3\inƯ\left(2\right)=\left\{\pm1;\pm3\right\}\)
Ta có bảng:
| x-3 | -1 | -3 | 1 | 3 |
| x | 2 | 0 | 4 | 6 |
Vậy \(x\in\left\{2;0;4;6\right\}\)

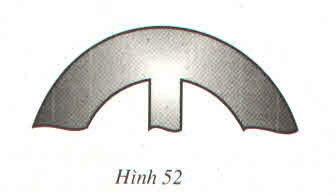
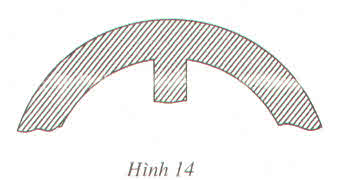
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Hướng dẫn:
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A

- Lấy 3 điểm A, B, C bất kì trên đường viền. Ba điểm này tạo thành tam giác ABC và tâm và bán kính đường tròn ngoại tiếp tam giác này chính là tâm và bán kính của đường viền.
- Vẽ trung trực của 2 cạnh AB, BC, chúng cắt nhau tại O. Từ tính chất đường trung trực suy ra OA = OB = OC
Do đó O chính là tâm đường tròn này. Khi đó OA hoặc OB hoặc OC chính là bán kính cần xác định.

Ta có:\(\left(-5a^2b^4c^6\right)^7-\left(9a^3bc^5\right)^8=0\)
\(\left(-5\right)^7a^{14}b^{28}c^{42}-9^8a^{24}b^8c^{40}=0\)
Vì \(a^{14}b^{28}c^{42}\ge0\Rightarrow\left(-5\right)^7a^{14}b^{28}c^{42}\le0\)
\(a^{24}b^8c^{40}\ge0\Rightarrow9^8a^{24}b^8c^{40}\ge0\)
\(\Rightarrow\left(-5\right)^7a^{14}b^{28}c^{42}-9^8a^{24}b^8c^{40}\le0\)
Mà VP=0
Dấu "=" xảy ra khi
\(\left(-5\right)^7a^{14}b^{28}c^{42}=0\) và \(9^8a^{24}b^8c^{40}=0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow A=a+b+c=0+0+0=0\)


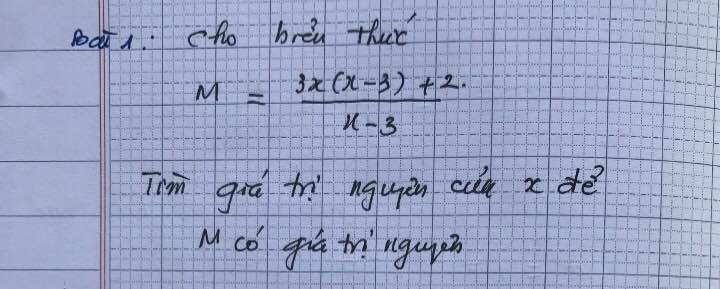
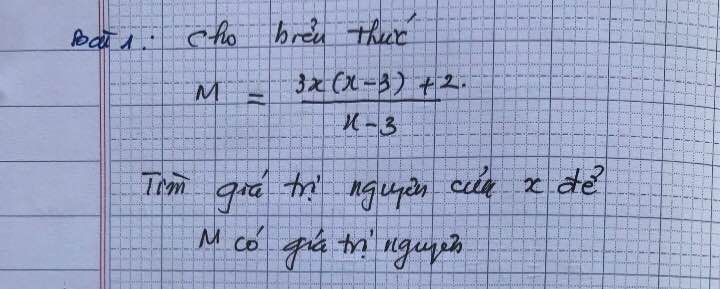







Để M nguyên thì \(x-3\in\left\{1;-1;2;-2\right\}\)
hay \(x\in\left\{4;2;5;1\right\}\)