Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
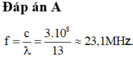
\(\lambda = c.T = c/f = \frac{3.10^8}{60.10^9}= 5.10^{-3}m.\)
Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)
Do E và B biến thiên cùng pha, cùng tần số nên:
\(\dfrac{E}{E_0}=\dfrac{B}{B_0}\Rightarrow \dfrac{4}{10}=\dfrac{B}{0,2}\)
\(\Rightarrow B = 0,08 T\)
Áp dụng quy tắc vEB với ngón cái, trỏ, ngón giữa theo thứ tự là v, E, B ta thấy B hướng xuống.
Khi tăng điện dung nên 2,5 lần thì dung kháng giảm 2,5 lần. Cường độ dòng trễ pha hơn hiệu điện thế \(\pi\text{/}4\) nên
\(Z_L-\frac{Z_C}{2,5}=R\)
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì
\(Z_LZ_C=R^2+Z^2_L\)
\(Z_LZ_C=\left(Z_L-\frac{Z_C}{2,5}\right)^2+Z^2_L\)
Giải phương trình bậc 2 ta được
\(Z_C=\frac{5}{4}Z_L\) hoặc \(Z_C=10Z_L\) (loại vì Zl-Zc/2.5=R<0)
\(R=\frac{Z_L}{2}\)
Vẽ giản đồ vecto ta được \(U\) vuông góc với \(U_{RL}\) còn \(U_C\) ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi \(U_L\) và \(U_{LR}\)
\(\tan\alpha=\frac{R}{Z_L}=0,5\)
\(\sin\alpha=1\text{/}\sqrt{5}\)
\(U=U_C\sin\alpha=100V\)
\(U_o=U\sqrt{2}=100\sqrt{2}V\)
chọn C
Gọi hình chiếu của điểm M trên AB là N, trung điểm của AB là O, đặt ON = x \(\Rightarrow\) \(AM=\sqrt{4+\left(4-x\right)^2}\)\(,BM=\sqrt{4+\left(4+x\right)^2}\)
\(\vartheta BM=\frac{2\pi BM}{\lambda}\)
\(\vartheta AM=\frac{2\pi AM}{\lambda}\)
\(\Rightarrow\frac{2\pi}{\lambda}\left(MB-MA\right)=\left(2k+1\right)\lambda\pi\)
Min khi k = 0 \(\Leftrightarrow\sqrt{4+\left(4+x\right)^2}-\sqrt{4+\left(4-x\right)^2}\)\(=1\Rightarrow x\approx0,56\left(cm\right)\)
chọn đáp án A
1/ Các đáp án B, C, D chỉ đúng khi các điểm này nằm trên cùng một phương truyền sóng.
\(\rightarrow\) Chọn đáp án A
2/ Khi các sóng truyền từ không khí vào nước thì tần số sóng không đổi còn bước sóng thay đổi sao cho \(f=\frac{v}{\lambda}=\)const .Khi truyền từ không khí vào nước vận tốc của sóng âm tăng nên bước sóng sẽ tăng, vận tốc của sóng ánh sáng giảm nên bước sóng sẽ giảm.
\(\rightarrow\)Chọn đáp án B
Ta có: \(\dfrac{2\pi.x}{\lambda}=0,02\pi.x\)
\(\Rightarrow \lambda=\dfrac{2}{0,02}=100 cm\)
