Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
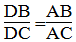
Suy ra:
Suy ra:
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)
b. Ta có: SABC =1/2.AB.AC =1/2.AH.BC
Suy ra: AB.AC = AH.BC
Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90o
Theo định lí Pi-ta-go, ta có: AB2 = AH2 + HB2
Suy ra: HB2 = AB2 - AH2 = 122 - (9,6)2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 607 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠(AHD) = 90o
Theo định lí Pi-ta-go, ta có:
AD2 = AH2 + HD2 = (9,6)2 + (1,37)2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)

A B C H D E F
a) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta được:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Xét tam giác ABC có AD là đường phân giác trong của tam giác ABC (gt)
\(\Rightarrow\frac{BD}{DC}=\frac{AB}{AC}\left(tc\right)\)
\(\Rightarrow\frac{BD}{DC}=\frac{3}{4}\)
\(\Rightarrow\frac{BD}{3}=\frac{DC}{4}=\frac{BD+DC}{3+4}\frac{10}{7}\)(tính chất của dãy tỉ số bằng nhau )
\(\Rightarrow\hept{\begin{cases}BD=\frac{10}{7}.3=\frac{30}{7}\left(cm\right)\\DC=\frac{10}{7}.4=\frac{40}{7}\left(cm\right)\end{cases}}\)
b)Ta có: \(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC\)
\(\Rightarrow AB.AC=AH.BC\left(đpcm\right)\)
c) Xét tam giác ADB có DE là đường phân giác trong của tam giác ADB(gt)
\(\Rightarrow\frac{EA}{EB}=\frac{AD}{BD}\left(tc\right)\)
Xét tam giác ADC có DF là đường phân giác trong của tam giác ADC (gt)
\(\Rightarrow\frac{FC}{FA}=\frac{DC}{DA}\left(tc\right)\)
\(\Rightarrow\frac{EA}{EB}.\frac{DB}{DC}.\frac{FC}{FA}=\frac{AD}{BD}.\frac{DB}{DC}.\frac{DC}{DA}=1\left(đpcm\right)\)

A B C H D
Bài làm:
a) Xét 2 tam giác: \(\Delta ABC\)và \(\Delta HBA\)có:
\(\hept{\begin{cases}\widehat{ABC}chung\\\widehat{AHB}=\widehat{BAC}=90^0\end{cases}}\)
=> \(\Delta ABC\)đồng dang với \(\Delta HBA\)(G.G)
b) \(\Delta AHB\)đồng dạng với \(\Delta CAB\)(G.G) vì:
\(\hept{\begin{cases}\widehat{AHB}=\widehat{AHC}=90^0\\\widehat{BAH}=\widehat{ACH}=90^0-\widehat{HAC}\end{cases}}\)
=> \(\frac{BH}{AH}=\frac{AH}{HC}\)\(\Leftrightarrow AH^2=BH.HC\)
c) Vì tam giác ABC vuông tại A nên theo định lý Py-ta-go, ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
Theo phần a, \(\Delta ABC\)đồng dạng với \(\Delta HBA\)(G.G)
=> \(\frac{BA}{AH}=\frac{BC}{AC}\Rightarrow AH=\frac{AB.AC}{BC}=\frac{48}{10}=4.8\left(cm\right)\)
Mà theo phần b, \(AH^2=BH.HC\)\(\Leftrightarrow BH.HC=4.8^2=23.04\Leftrightarrow HC=\frac{23.04}{HB}\)
Thay vào ta có: \(HB+HC=BC\)
\(\Leftrightarrow HB+\frac{23.04}{HB}=10\)
Từ đó ta giải phương trình ẩn HB ra, \(HB=3.6\left(cm\right)\)
=> \(HC=10-3.6=6.4\left(cm\right)\)
d) Đề bạn viết nhầm phải là cho AD là phân giác của tam giác ABC.
Áp dụng tính chất của tia phân giác trong tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{4}\Leftrightarrow DC=\frac{4}{3}BD\)
Thay vào đó, ta giải phương trình sau:
\(BD+DC=BC\Leftrightarrow BD+\frac{4}{3}BD=10\)
Từ đó ta giải phương trình ẩn BD => \(BD=\frac{30}{7}cm\)
=> Diện tích tam giác ABD là:
\(S\Delta ABD=\frac{AH.BD}{2}=\frac{4.8\times\frac{30}{7}}{2}=\frac{72}{7}\left(cm^2\right)\)
Học tốt!!!!

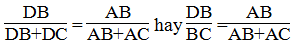
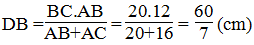
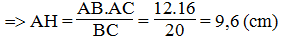
Lời giải:
a) Vì tam giác $ABC$ vuông tại $A$ nên:
$S_{ABC}=\frac{AB.AC}{2}$
Mặt khác: $S_{ABC}=\frac{AH.BC}{2}$
$\Rightarrow AB.AC=AH.BC$ (đpcm)
b) Áp dụng định lý Pitago cho tam giác $ABC$ vuông:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
Áp dụng định lý Pitago cho tam giác $ABH$ vuông:
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BD+DC}=\frac{BD}{BC}=\frac{3}{3+4}$
$\Rightarrow BD=BC.\frac{3}{7}=\frac{60}{7}$ (cm)
$DC=BC-BD=20-\frac{60}{7}=\frac{80}{7}$ (cm)
Hình vẽ: