Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sửa đề tam giác DEF là tam giác gì ?
Vì tam giác DEF có DM là đường trung tuyến
đồng thời là đường phân giác
nên tam giác DEF cân tại D

a: góc KBA=1/2*góc ABC
góc DAC=1/2*góc HAC
mà góc ABC=góc HAC
nên góc KBA=góc DAC
góc BAD+góc CAD=90 độ
góc BDA+góc DAH=90 độ
mà góc CAD=góc DAH
nên góc BAD=góc BDA
=>ΔBAD cân tại B
=>BK vuông góc AD
b: BO là phân giác của góc BA
=>OA=OE
CO là trung trực của AD
=>OA=OD
=>OE=OD
=>OA=OE
=>góc OAE=góc OEA
Vẽ Ox là tia đối của tia OA
góc xOE=góc OAE+góc OEA=2*góc xAE
Chứng minh tương tự, ta được: góc xOD=2*góc xAD
=>góc DOE=2*góc DAE
=2*1/2(góc BAH+góc HAC)=90 độ

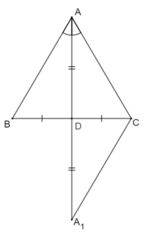
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)

⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 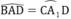 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
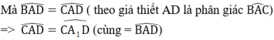
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

a) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
AH=AK(gt)
Do đó: ΔAHD=ΔAKD(cạnh huyền-cạnh góc vuông)
b) Vì △AHD=△AKD nên DH=DK
Mà AH=AK
Kết hợp 2 điều này lại suy ra AD là trung trực của HK
Ta có đpcm

Xét ΔABC có
AM vừa là đường phân giác, vừa là đường trung tuyến
nên ΔABC cân tại A

GTvà KL bạn tự ghi nha:
a)Xét ΔABH và ΔDBH, có:
Góc BHA=góc BHD=90 độ
BH là cạnh chung
AH=DH(gt)
=>ΔABH=ΔDBH (c.g.c)
b)Ta có:
góc ABH=gócHBD( vì ΔABH=ΔDBH)
Do đó BC là tia phân giác của góc ACD
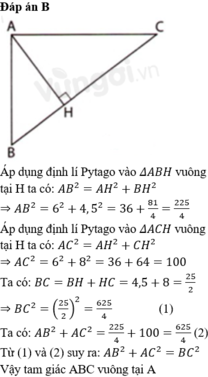
Tam giác ABC cân tại A
tam giác ABC là tam giác cân nhé