Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

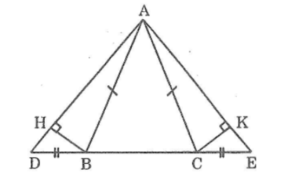
Xét ΔABH và ΔACK, ta có:
AB = AC (gt)
∠(AHB) =∠(AKC) =90o
BH=CK ( chứng minh trên)
Suy ra: ΔABH= ΔACK (cạnh huyền– cạnh góc vuông)

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: \(\widehat{D}=\widehat{E}\)
Xét ΔHDB vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHDB=ΔKEC
Suy ra: BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
Do đó: ΔAHB=ΔAKC

a) Do ΔABC cân tại A
=> AB = AC; góc ABC=góc ACB
Lại có: góc ABC+ góc ABD = 180o (kề bù)
góc ACB + góc ACE = 180o (kề bù)
=> góc ABD = góc ACE
Xét ΔADB và ΔAEC có:
góc BAD = góc CAE (gt)
AB = AC (cmt)
góc ABD = góc ACE (cmt)
=> ΔADB = ΔAEC (g.c.g)
=> BD = CE (2 cạnh tg ứng) đpcm
b) Vì ΔADB = ΔAEC (câu a)
=> góc ADB = góc AEC (2 góc t/ư)
hay góc HDB = góc KEC
Xét ΔBHD vuông tại H và ΔCKE vuông tại E có:
BD = CE (câu a)
góc HDB = góc KEC(cmt)
=> ΔBHD = ΔCKE (ch - gn)
=> BH = CK (2 cạnh tg ứng) (đpcm)

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
DO đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
BH=CK
Do đó: ΔABH=ΔACK

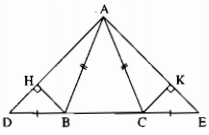
a) Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
b) Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
c) Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
DB=CE(gt)
\(\widehat{HDB}=\widehat{KEC}\)(hai góc ở đáy của ΔADE cân tại A)
Do đó: ΔDHB=ΔEKC(cạnh huyền-góc nhọn)
d) Ta có: ΔDHB=ΔEKC(cmt)
nên \(\widehat{HBD}=\widehat{KCE}\)(hai góc tương ứng)
mà \(\widehat{HBD}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCE}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)
e) Xét ΔABO và ΔACO có
AB=AC(ΔABC cân tại A)
AO chung
BO=CO(ΔOBC cân tại O)
Do đó: ΔABO=ΔACO(c-c-c)
nên \(\widehat{BOA}=\widehat{COA}\)(hai góc tương ứng)
mà tia OA nằm giữa hai tia OB,OC
nên OA là tia phân giác của \(\widehat{BOC}\)(đpcm)
chả hiểu tia đối là gì.