K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
19 tháng 1 2022
Đường thẳng song song với d1 và d2 là:
(d3): 2x - 3y + c (với c khác 1 và c khác 1,5)
17 tháng 1 2021
Ta thấy d1 // d2 do chúng có cùng vecto pháp tuyến là
\(\overrightarrow{n}=\left(2;3\right)\)
d đối xứng với d1 qua d2 ⇒ d // d1 // d2 (1)
và d đi qua đầu mút còn lại của một đoạn thẳng có một đầu mút nằm trên d1 và trung điểm của đoạn thẳng ấy nằm trên d2 (2)
(1) ⇒ d có vecto pháp tuyến là \(\overrightarrow{n}=\left(2;3\right)\)
Gọi M (1; 1) ∈ d1 và N (1; -1) ∈ d2. Gọi giao điểm của MN với d là P
Từ (2) ⇒ N là trung điểm của MP
⇒ P(1; -3)
Vậy d đi qua P(1; -3) và có vecto pháp tuyến là \(\overrightarrow{n}=\left(2;3\right)\)
⇒ Phương trình của d là : 2 (x - 1) + 3 (y + 3) = 0
hay 2x + 3y + 7 = 0
CM
4 tháng 3 2019
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
24 tháng 2 2023
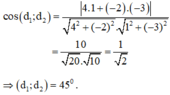
M thuộc (d1) nên M(1-2t;1+t)
Theo đề, ta có: d(M;d2)=d(M;d3)
=>\(\dfrac{\left|\left(1-2t\right)\cdot3+\left(1+t\right)\cdot4-4\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|\left(1-2t\right)\cdot4+\left(1+t\right)\cdot\left(-3\right)+2\right|}{\sqrt{4^2+\left(-3\right)^2}}\)
=>|-6t+3+4t+4-4|=|4-8t-3t-3+2|
=>|-2t+3|=|-11t+3|
=>-2t+3=-11t+3 hoặc -2t+3=11t-3
=>t=0 hoặc t=6/13
=>M(1;1); M(1/13; 19/13)
CM
13 tháng 2 2017
ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
Gọi đường tròn tâm \(I\left(a;b\right)\Rightarrow d\left(I;d_1\right)=d\left(I;d_2\right)\)
\(\Rightarrow\dfrac{\left|3a-4b+1\right|}{5}=\dfrac{\left|4a+3b-7\right|}{5}\)
\(\Rightarrow\left[{}\begin{matrix}3a-4b+1=4a+3b-7\\3a-4b+1=-4a-3b+7\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=-7b+8\\b=7a-6\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}I\left(-7b+8;b\right)\\I\left(a;7a-6\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}IA^2=\left(-7b+6\right)^2+\left(b-3\right)^2\\IA^2=\left(a-2\right)^2+\left(7a-9\right)^2\end{matrix}\right.\)
\(IA^2=d^2\left(I;d_1\right)\Rightarrow\left[{}\begin{matrix}\left(-7b+6\right)^2+\left(b-3\right)^2=\left(b-1\right)^2\\\left(a-2\right)^2+\left(7a-9\right)^2=\left(a-1\right)^2\end{matrix}\right.\)
Giờ giải pt bậc 2 là được
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2019
Giao điểm A của d1 và d2 là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-2y+5=0\\2x-3y+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow A\left(1;3\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-1\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-15=0\)
Yêu cầu của đề là gì vậy bạn?