K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8 2023
1: \(=\left[\left(\sqrt{2}+\sqrt{3}\right)^2-5\right]\cdot\left[\left(\sqrt{5}\right)^2-\left(\sqrt{2}-\sqrt{3}\right)^2\right]\)
\(=2\sqrt{6}\left(5-5+2\sqrt{6}\right)=2\sqrt{6}\cdot2\sqrt{6}=24\)
2: \(A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\)
=>\(A^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\cdot\sqrt{16-10-2\sqrt{5}}\)
\(=8+2\cdot\sqrt{6-2\sqrt{5}}\)
\(=8+2\left(\sqrt{5}-1\right)=6+2\sqrt{5}\)
=>\(A=\sqrt{5}+1\)
15 tháng 3 2022
Ta có \(\dfrac{a^3}{a^2+b^2}=a-\dfrac{ab^2}{a^2+b^2}\ge a-\dfrac{ab^2}{2ab}=a-\dfrac{b}{2}=\dfrac{2a-b}{2}\)(áp dụng cosi cho \(a^2+b^2\ge2ab\))
\(\dfrac{b^3}{b^2+1}=b-\dfrac{b}{b^2+1}\ge b-\dfrac{b}{2b}=b-\dfrac{1}{2}=\dfrac{2b-1}{2}\)(áp dụng cosi cho\(b^2+1\ge2b\))
\(\dfrac{1}{a^2+1}=1-\dfrac{a^2}{a^2+1}\ge1-\dfrac{a^2}{2a}=1-\dfrac{a}{2}=\dfrac{2-a}{2}\)( áp dụng cosi cho \(a^2+1\ge2a\))
Cộng vế theo vế
\(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+1}+\dfrac{1}{a^2+1}\ge\dfrac{2a-b+2b-1+2-a}{2}\)\(\ge\dfrac{a+b+1}{2}\left(đpcm\right)\)
Dấu "=" xảy ra <=> a=b=1
11 tháng 7 2023
4:
a: cos^2a=1-(1/2)^2=1-1/4=3/4
=>\(cosa=\dfrac{\sqrt{3}}{2}\)
\(tana=\dfrac{1}{2}:\dfrac{\sqrt{3}}{2}=\dfrac{1}{\sqrt{3}}\)
\(cota=1:\dfrac{1}{\sqrt{3}}=\sqrt{3}\)
b: sin^2a=1-(3/4)^2=1-9/16=7/16
=>\(sina=\dfrac{\sqrt{7}}{4}\)
\(tana=\dfrac{\sqrt{7}}{4}:\dfrac{3}{4}=\dfrac{\sqrt{7}}{3}\)
\(cota=1:\dfrac{\sqrt{7}}{3}=\dfrac{3}{\sqrt{7}}\)
22 tháng 6 2023
a: \(C=\dfrac{x+\sqrt{x}-x+\sqrt{x}}{x-1}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{2}{\sqrt{x}+1}\)
b: C<1
=>\(\dfrac{2-\sqrt{x}-1}{\sqrt{x}+1}< 0\)
=>1-căn x<0
=>x>1
22 tháng 8 2023
AM nhỏ nhất khi MA là khoảng cách từ M xuống (d)
y=2x+3
=>2x-y+3=0
Gọi (d') là đường thẳng đi qua M và vuông góc (d)
=>MA nhỏ nhất là khi A là giao của (d) với (d')
(d') vuông góc (d)
=>(d'): y=-1/2x+b
Thay x=4 và y=2 vào (d'), ta được:
b-1/2*4=2
=>b-2=2
=>b=4
=>(d'): y=-1/2x+4
Tọa độ A là;
-1/2x+4=2x+3 và y=2x+3
=>-5/2x=-1 và y=2x+3
=>x=2/5 và y=4/5+3=19/5
16 tháng 2 2022
\(x^2+\sqrt{5}x-10=0\)
\(\Delta=5-4\left(-10\right)=45>0\)
Vậy pt có nghiệm pb
\(x_1=\dfrac{-\sqrt{5}-3\sqrt{5}}{2}=-2\sqrt{5};x_2=\dfrac{-\sqrt{5}+3\sqrt{5}}{2}=\sqrt{5}\)
NH
31 tháng 1 2023
sửa lại nhé
\(\left\{{}\begin{matrix}3\left(x-y\right)-y=11\\x-2\left(x+5y\right)=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}3x-3y-y=11\\x-2x-10y=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}3x-4y=11\\-x-10y=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)
Y
31 tháng 1 2023
\(\Leftrightarrow\left\{{}\begin{matrix}3x-3y-y=11\\x-2x-10y=-15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-4y=11\\-x-10y=-15\left(1\right)\end{matrix}\right.\)
Nhân \(-3\) vào \(\left(1\right)\)
\(\left\{{}\begin{matrix}3x-4y=11\left(2\right)\\3x+30y=45\left(3\right)\end{matrix}\right.\)
Lấy \(\left(2\right)-\left(3\right)\) :
\(\Leftrightarrow3x-3x-4y-30y=11-45\)
\(\Leftrightarrow-34y=-34\)
\(\Leftrightarrow x=1\)
Lấy \(x=1\) thay vào \(\left(2\right)\) : \(3.1-4y=11\Leftrightarrow y=2\)
Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(1;2\right)\)
15 tháng 11 2023
10: \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=\left(\sqrt{3-\sqrt{5}}\right)^2+\left(\sqrt{3+\sqrt{5}}\right)^2+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{9-5}\)
\(=6+2\cdot2=10\)
11: \(\left(\sqrt{\sqrt{7}+\sqrt{3}}+\sqrt{\sqrt{7}-\sqrt{3}}\right)^2\)
\(=\left(\sqrt{\sqrt{7}+\sqrt{3}}\right)^2+\left(\sqrt{\sqrt{7}-\sqrt{3}}\right)^2+2\cdot\sqrt{\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)}\)
\(=\sqrt{7}+\sqrt{3}+\sqrt{7}-\sqrt{3}+2\cdot\sqrt{7-3}\)
\(=2\sqrt{7}+2\cdot2=2\sqrt{7}+4\)
12: \(\left(\sqrt{\sqrt{11}+\sqrt{7}}-\sqrt{\sqrt{11}-\sqrt{7}}\right)^2\)
\(=\left(\sqrt{\sqrt{11}+\sqrt{7}}\right)^2+\left(\sqrt{\sqrt{11}-\sqrt{7}}\right)^2-2\cdot\sqrt{\left(\sqrt{11}-\sqrt{7}\right)\left(\sqrt{11}+\sqrt{7}\right)}\)
\(=\sqrt{11}+\sqrt{7}+\sqrt{11}-\sqrt{7}-2\cdot\sqrt{11-7}\)
\(=2\sqrt{11}-4\)
13:
\(\sqrt{\sqrt{2}-1}\cdot\sqrt{2-\sqrt{3-\sqrt{2}}}\cdot\sqrt{2+\sqrt{3-\sqrt{2}}}\)
\(=\sqrt{\sqrt{2}-1}\cdot\sqrt{4-\left(3-\sqrt{2}\right)}\)
\(=\sqrt{\sqrt{2}-1}\cdot\sqrt{\sqrt{2}+1}\)
\(=\sqrt{2-1}=1\)
14:
\(\sqrt{4+\sqrt{8}}\cdot\sqrt{2+\sqrt{2+\sqrt{2}}}\cdot\sqrt{2-\sqrt{2+\sqrt{2}}}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{\left(2+\sqrt{2+\sqrt{2}}\right)\left(2-\sqrt{2+\sqrt{2}}\right)}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{4-2-\sqrt{2}}\)
\(=\sqrt{\left(4+2\sqrt{2}\right)\left(2-\sqrt{2}\right)}\)
\(=\sqrt{8-4\sqrt{2}+4\sqrt{2}-4}=\sqrt{4}=2\)
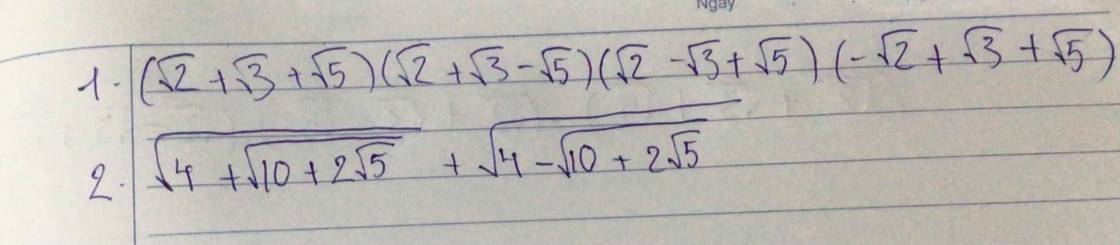
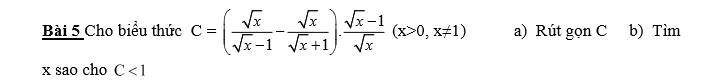
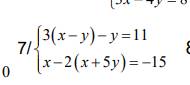
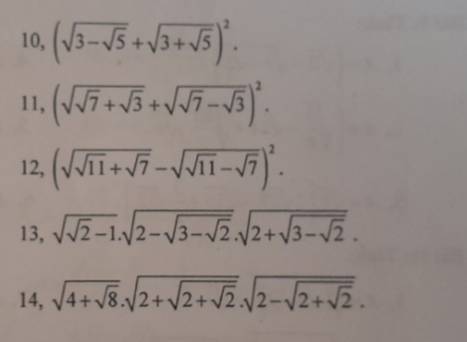
a) Gọi phương trình đường thẳng (d) đi qua B và C là \(\left(d\right):y=ax+b\)(*)
Thay \(x_B=2;y_B=-2\)vào (*), ta có: \(-2=2a+b\Rightarrow b=-2a-2\)(1)
Thay \(x_C=1;y_C=-3\)vào (*), ta có: \(-3=a+b\Rightarrow b=-a-3\)(2)
Từ (1) và (2) suy ra \(-2a-2=-a-3\Leftrightarrow-a+2a=-2+3\Leftrightarrow a=1\)
\(\Rightarrow b=-a-3=-1-3=-4\)
Vậy phương trình đường thẳng (d) là \(\left(d\right):y=x-4\)
b) Bạn này có thể tự vẽ được.
c) Giả sử (d) cắt trục Ox tại D, cắt trục Oy tại E. Gọi tọa độ của D và E lần lượt là \(\left(x_D;y_D\right)\)và \(\left(x_E;y_E\right)\)
Dễ thấy rằng \(y_D=0\)vì D nằm trên trục Ox; \(x_E=0\)vì E nằm trên trục Oy.
Mà (d) chính là đường thẳng \(\left(d\right):y=x-4\)(**)
Thay \(y=y_D=0;x=x_D\)vào (**), ta có: \(0=x_D-4\Rightarrow x_D=4\)
Vì D nằm trên trục Ox nên ta có \(OD=|x_D|=|4|=4\left(đvđd\right)\)
Bằng cách tương tự ta cũng có thể tính được \(OE=4\left(đvđd\right)\)
Xét \(\Delta ODE\)vuông tại O có \(\tan EDO=\frac{OE}{OD}=\frac{4}{4}=1\Rightarrow\widehat{EDO}=45^0\)
Vậy góc tạo bởi (d) và trục Ox bằng \(45^0\)
d) Vì A, B, C thẳng hàng nên A phải nằm trên đường thẳng BC. Mà đường thẳng BC chính là đường thẳng (d) nên A phải thuộc đường thẳng (d).
Thay \(y=2;x=x_A\)vào phương trình đường thẳng\(\left(d\right):y=x-4\)ta có:
\(2=x_A-4\Rightarrow x_A=6\)
Vậy để A, B, C thẳng hàng thì \(x_A=6\)
Help :(((