K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
cứu tui mn ơi
1 tháng 2 2022
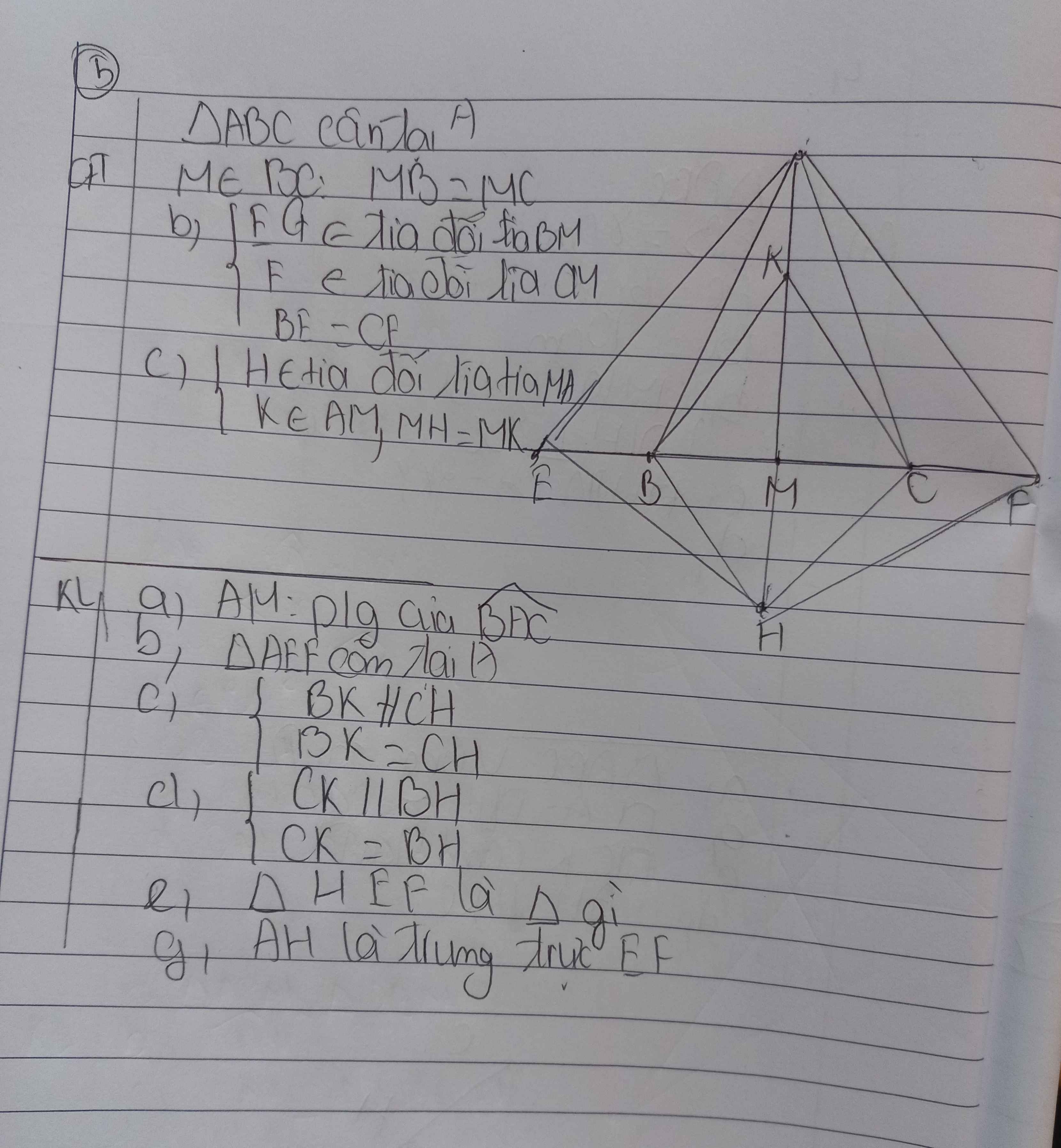
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Xét ΔABE và ΔACF có
AB=AC
\(\widehat{ABE}=\widehat{ACF}\)
BE=CF
Do đó: ΔABE=ΔACF
c: Xét tứ giác BKCH có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BKCH là hình bình hành
Suy ra: BK//CH; BK=CH
d: Ta có: BKCH là hình bình hành
nên CK//BH; CK=BH
10 tháng 5 2022
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Xét ΔBDF và ΔEDC có
\(\widehat{BDF}=\widehat{EDC}\)
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
Do đó: ΔBDF=ΔEDC
9 tháng 4 2022
a: Xét ΔABE và ΔHBE có
BA=BH
\(\widehat{ABE}=\widehat{HBE}\)
BE chung
Do đó: ΔABE=ΔHBE
b: Ta có: ΔABE=ΔHBE
nên BA=BH và EA=EH
=>BE là đường trung trực của AH
d: ta có: EA=EH
mà EH<EC
nên EA<EC
30 tháng 7 2023
a: DE<EF
=>góc F<góc D
b: Xét ΔDKE vuông tại K và ΔDKI vuông tại K có
DK chung
KE=KI
=>ΔDKE=ΔDKI
c: ΔDKE=ΔDKI
=>DE=DI
=>ΔDEI cân tại D
mà góc DEI=60 độ
nên ΔDEI đều
13 tháng 5 2022
Lớp 7 học cái này rồi bạn
Cái này chỉ đơn giản là AB=0 thì A=0 hoặc B=0 thôi
N
13 tháng 11 2021
Bài 6:
Gọi số giấy vụn 3 lớp thu được lần lượt là: \(a,b,c\left(a,b,c>0\right)\)
Áp dụng TCDTSBN:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{150}{15}=10\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\cdot10=30\left(kg\right)\\b=5\cdot10=50\left(kg\right)\\c=7\cdot10=70\left(kg\right)\end{matrix}\right.\)
13 tháng 11 2021
Bài 4:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{-21}{7}=-3\)
Do đó: x=-6; y=-15
TK
1
29 tháng 7 2023
1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3
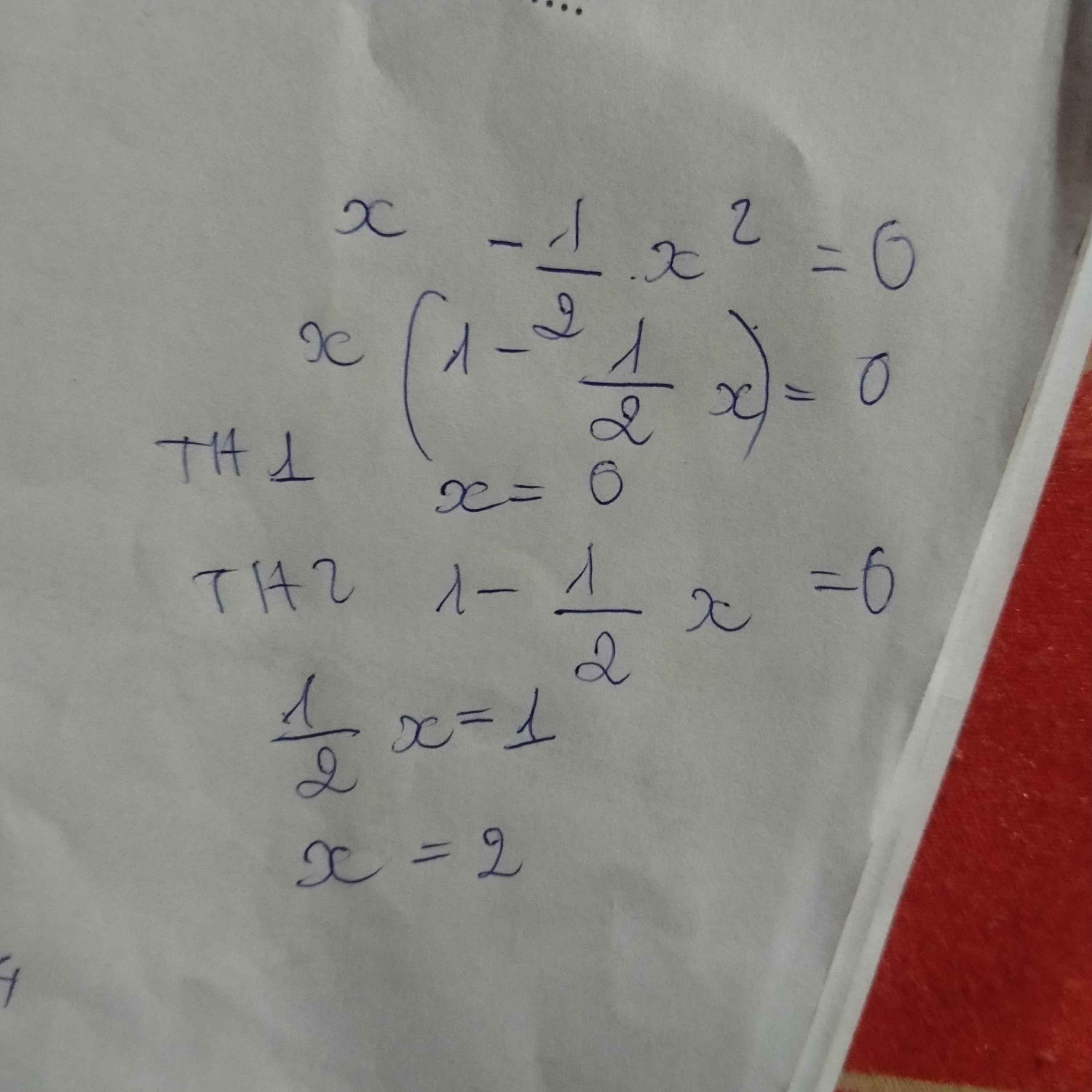
ΔAED vuông tại E
=>AE<AD
ΔCFD vuông tại F
=>CF<CD
AE<AD
CF<CD
Do đó: AE+CF<AD+CD=AC