Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chiều rộng của mảnh vườn hình chữ nhật là:
\(\dfrac{21}{4}\) : \(\dfrac{7}{3}\) = \(\dfrac{9}{4}\) (m)
Chu vi của mảnh vườn hìn chữ nhật là:
(\(\dfrac{21}{4}\) + \(\dfrac{9}{4}\)) x 2 = 15 (m)
Diện tích của mảnh vườn hình chữ nhật là:
\(\dfrac{21}{4}\) x \(\dfrac{9}{4}\) = \(\dfrac{189}{16}\) (m2)
b; Số tiền thu được khi trồng hoa để bán trên mảnh đất hình chữ nhật đó là:
80 000 x \(\dfrac{189}{16}\) = 945 000 (đồng)
KL...
Bài 5:
a, Chiều rộng mảnh vườn:
\(\dfrac{21}{4}:\dfrac{7}{3}=\dfrac{9}{4}\left(m\right)\)
Chu vi mảnh đất:
\(2\times\left(\dfrac{21}{4}+\dfrac{9}{4}\right)=15\left(m\right)\)
Diện tích mảnh đất:
\(\dfrac{21}{4}\times\dfrac{9}{4}=\dfrac{189}{16}\left(m^2\right)\)
b, Số tiền thu được khi bán hoa:
\(\dfrac{189}{16}\times80000=945000\left(đồng\right)\)

Bài 5:
30 phút = \(\dfrac{1}{2}\) giờ
Thời gian gia đình bạn Tuấn đi từ Hà Nội tới Phan Thiết tới là:
\(\dfrac{13}{4}\) + \(\dfrac{1}{2}\) + \(\dfrac{13}{3}\) = \(\dfrac{97}{12}\) giờ
\(\dfrac{95}{12}\) giờ = 8 giờ 5 phút
b; Gia đình bạn Tuấn đến thành Phố Phan Thiết lúc:
6 giờ + 8 giờ 5 phút = 14 giờ 5 phút
Kl...
Bài 6:
a; -3 - \(\dfrac{2}{5}\) ≤ \(x\) ≤ \(\dfrac{1}{2}\) - \(\dfrac{-3}{4}\)
- \(\dfrac{17}{5}\) ≤ \(x\) ≤ \(\dfrac{5}{4}\)
-3,4 ≤ \(x\) ≤ 1,25
Vì \(x\) là số nguyên nên \(x\) \(\in\) {-3; -2; -1; 0; 1}

Bài 1 mk ko vẽ hình đc thông cảm trang này khó vẽ quá
bài 2:
B=(1 - 1/2).(1 - 1/3)....(1 - 1/20)
B=\(\frac{1}{2}\cdot\frac{2}{3}\cdot...\cdot\frac{19}{20}\)
B=\(\frac{1}{20}\)

theo đầu bài \(\widehat{A_2}\)=\(60^0\)\(\Rightarrow\)\(\widehat{A_4}\)= \(60^0\)( đối đỉnh)
ta có \(\widehat{A_3}\)+\(\widehat{A_4}\)=\(180^0\)(góc bẹt) mà \(\widehat{A_4}\)=\(60^0\)\(\Rightarrow\)\(\widehat{A_3}\)= \(180^0\)- \(60^0\)=\(120^0\)
ta có \(\widehat{A_3}\)= \(\widehat{A_1}\)= \(120^0\)( đối đỉnh)
a, góc A4=góc A2=60 độ (hai góc đối đỉnh)
góc A4+góc A1=180 độ (kề bù)
=>60 độ+góc A1=180 độ
=> góc A1=180 độ-60 độ=120 độ
mà góc A1= góc A3=120 độ.
vậy góc A4=60độ, A1=A3=120độ
b, góc B1 + góc A4=180 độ (hai góc trong cùng phía)
=>góc B1+60 độ=180 độ
=> góc B1=180 độ - 60 độ=120 độ
mà góc B1=góc B3 =120(2 góc đối đỉnh)
lại có: B1+góc B4=180 độ (trong cùng phía)
=>góc B4=180 độ-120 độ=60 độ
mà góc B4= góc B2=60 độ
vậy B1=120 độ, B3=120 độ, B2=B4=60 độ
chúc bn hok tốt ![]()

bài 3:
a: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=5\left(1+5+5^2+\cdots+5^{19}\right)\) ⋮5
b: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{19}+5^{20}\right)\)
\(=5\left(1+5\right)+5^3\left(1+5\right)+\cdots+5^{19}\left(1+5\right)\)
\(=6\left(5+5^3+\cdots+5^{19}\right)\) ⋮6
c: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)+\cdots+\left(5^{17}+5^{18}+5^{19}+5^{20}\right)\)
\(=5\left(1+5+5^2+5^3\right)+5^5\left(1+5+5^2+5^3\right)+\cdots+5^{17}\left(1+5+5^2+5^3\right)\)
\(=\left(1+5+5^2+5^3\right)\left(5+5^5+\cdots+5^{17}\right)=156\cdot\left(5+5^5+\cdots+5^{17}\right)\)
\(=13\cdot12\cdot\left(5+5^5+\cdots+5^{17}\right)\) ⋮13
Bài 2:
a: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=3\left(1+3+3^2+3^3+\cdots+3^{119}\right)\) ⋮3
b: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+\cdots+\left(3^{119}+3^{120}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+\cdots+3^{119}\left(1+3\right)\)
\(=4\left(3+3^3+\cdots+3^{119}\right)\) ⋮4
c: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+\cdots+\left(3^{118}+3^{119}+3^{120}\right)\)
\(=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+\cdots+3^{118}\left(1+3+3^2\right)\)
\(=13\left(3+3^4+\cdots+3^{118}\right)\) ⋮13
Bài 1:
a: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=2\left(1+2+2^2+\cdots+2^{19}\right)\) ⋮2
b: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+\cdots+\left(2^{19}+2^{20}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+\cdots+2^{19}\left(1+2\right)\)
\(=3\left(2+2^3+\cdots+2^{19}\right)\) ⋮3
c: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+\cdots+\left(2^{17}+2^{18}+2^{19}+2^{20}\right)\)
\(=2\left(1+2+2^2+2^3\right)+2^5\left(1+2+2^2+2^3\right)+\cdots+2^{17}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+\ldots+2^{17}\right)=5\cdot3\cdot\left(2+2^5+\cdots+2^{17}\right)\) ⋮5
Bài 1:
a; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
A = 2 x (1+ 2+ 2\(^2\) + ... + 2\(^{19}\))
A ⋮ 2(đpcm)
b; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
Xét dãy số: 1; 2;...; 20 đây là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Số số hạng của dãy số trên là:
(20 - 1) : 1+ 1 = 20(số)
Vì 20 : 2 = 10
Vậy nhóm hai số hạng liên tiếp của A vào nhau khi đó ta có:
A = (2+ 2\(^2\)) + (2\(^3\) + 2\(^4\)) + ... + (2\(^{19}+\) 2\(^{20}\))
A = 2.(1 + 2) + 2\(^3\).(1+ 2) + ... + 2\(^{19}\) .(1 + 2)
A = 2.3 + 2\(^3\).3 + ... + 2\(^{19}\).3
A = 3.(2+ 2\(^3\) + ... + 2\(^{19}\))
A ⋮ 3 (đpcm)
c; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
Xét dãy số: 1; 2; 3;...; 20
Dãy số trên có 20 số hạng:
Vì 20 : 4 = 5
Vậy nhóm 4 hạng tử của A thành một nhóm khi đó:
A = (2+ 2\(^2\) + 2\(^3\) + 2\(^4\)) + ... + (2\(^{17}+2^{18}+2^{19}+2^{20}\))
A = 2.(1 + 2 + 2\(^2\) + 2\(^3\)) + ... + 2\(^{17}\).(1 + 2 + 2\(^2\) + 2\(^3\))
A = (1+ 2 +2\(^2\) + 2\(^3\)).(2+ ...+ 2\(^{17}\))
A = (1 + 2 + 4 + 8).(2+ ...+ 2\(^{17}\))
A = (3+ 4 + 8).(2+ ...+ 2\(^{17}\))
A = (7 + 8)(2+ ...+ 2\(^{17}\))
A = 15.(2+ ...+ 2\(^{17}\))
A ⋮ 5(đpcm)

Bài 23:
a+4b⋮13
=>10(a+4b)⋮13
=>10a+40b⋮13
=>10a+b+39b⋮13
mà 39b⋮13
nên 10a+b⋮13

a) Ư(60):{ 1;2;3;4;5;6;10;12;15;20;30;60}
Ư(84):{ 1;2;4;6;7;12;14;21;42;84}
Ư(120):{ 1;2;3;4;5;6;8;10;12;15;20;24;30;40;60;120}
ƯC(60;84;120):{ 2;4;6;12}
nhưng vì x_> 6 nên x = 2,4,6
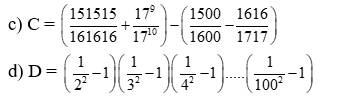


 Giúp em vs chứ em đau đầu lắm rồi 😭
Giúp em vs chứ em đau đầu lắm rồi 😭


 các bạn giúp mik trc 7h tối nay nha. Mik tick cho bạn nào nhanh và đúng nhé
các bạn giúp mik trc 7h tối nay nha. Mik tick cho bạn nào nhanh và đúng nhé
c) C=(151515/161616 + 17^9/17^10)-(1500/1600 - 1616/1717)
=(15/16 + 1/17)-(15/16 - 16/17)
= 15/16 ( 1/17 + 16/17)
=15/16 . 1 = 15/16
áp dụng đúng công thức là ra