
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì \(\left|3x-5\right|\ge0;\left(2y+5\right)^{208}\ge0;\left(4z-3\right)^{20}\ge0\)
Mà \(\left|3x-5\right|+\left(2y+5\right)^{208}+\left(4z-3\right)^{20}\le0\)
Do đó dấu \("="\Leftrightarrow\left\{{}\begin{matrix}3x-5=0\\2y+5=0\\4z-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=-\dfrac{5}{2}\\z=\dfrac{3}{4}\end{matrix}\right.\)

a, \(=2x^2y^2-xy^2-4+5x^2y\)
-> bậc 4
b, \(=\dfrac{2}{3}xy^4-xyz-2x^4y+1\)
-> bậc 5



Xét ΔABC và ΔAED có
AB=AE
BC=ED
AC=AD
Do đó: ΔABC=ΔAED

n đường thẳng đi qua điểm M tạo thành 2n tia chung gốc M
Lấy 1 tia trong 2n tia chung gốc M tạo với 2n-1 tia , còn lại 2n-1 góc
-> Có 2n tia thì có: 2n*(2n-1) góc
Vì mỗi góc được tính 2 lần
-> Có số góc là : 2n*(2n-1):2=n*(2n-1) góc
n đường thẳng đôi một phân biệt đi qua M tạo thành n góc bẹt
-> Có số góc nhỏ hơn góc bẹt là: n*(2n-1)-n=n*(2n-2)=n*(n-1)*2 ( góc )
Vì 2 góc là một cặp góc đối đỉnh
-> Có số góc đối đỉnh nhỏ hơn góc bẹt là :
n*(n-1)*2 : 2= n*(n-1) góc
Vậy có n*(n-1) cặp góc đối đỉnh nhỏ hơn góc bẹt.
b) Theo phần a) ta có:
n*(n-1)=930
Ta thấy: n và n-1 là hai số liên tiếp mà 930=31*30
=>n*(n-1)=31*30
=> n=31
Vậy n=31
Like ủng hộ mk nha!

Hình 2.
tEm vs t'Em'
tEn vs t'Em'
nEm' vs n'Em
nEm vs m'En'
tEm' vs t'Em
@Cỏ
#Forever

\(x^{2017}=\frac{x^{2017}-2}{3}\)
\(\Leftrightarrow3x^{2017}=x^{2017}-2\)
\(\Leftrightarrow2x^{2017}=-2\)
\(\Leftrightarrow x^{2017}=-1\)
\(\Leftrightarrow x=-1\)
\(x^{2017}=\frac{x^{2017}-2}{3}\)
\(\Leftrightarrow\frac{2x^{2017}+2}{3}=0\)
\(\Leftrightarrow2x^{2017}+2=0.3\)
\(\Leftrightarrow2x^{2017}+2=0\)
\(\Leftrightarrow2x^{2017}=0-2\)
\(\Leftrightarrow2x^{2017}=-2\)
\(\Leftrightarrow x^{2017}=\left(-1\right)^{\frac{1}{2017}}\)
x = 1

a) Ta có : 2017 - |x - 2017| = x
=> |x - 2017| = 2017 - x (1)
Điều kiện xác định : \(2017-x\ge0\Rightarrow2017\ge x\Rightarrow x\le2017\)
Khi đó (1) <=> \(\orbr{\begin{cases}x-2017=2017-x\\x-2017=-\left(2017-x\right)\end{cases}\Rightarrow\orbr{\begin{cases}2x=2017+2017\\x-2017=-2017+x\end{cases}\Rightarrow}\orbr{\begin{cases}2x=4034\\0x=0\end{cases}}}\)
\(\Rightarrow\orbr{\begin{cases}x=2017\\x\text{ thỏa mãn }\Leftrightarrow x\le2017\end{cases}}\Rightarrow x\le2017\)
b) Ta có : \(\hept{\begin{cases}\left(2x-1\right)^{2016}\ge0\forall x\\\left(y-\frac{2}{5}\right)^{2016}\ge\\\left|x+y+z\right|\ge0\forall x;y;z\end{cases}0\forall y}\Rightarrow\left(2x-1\right)^{2016}+\left(y-\frac{2}{5}\right)^{2016}+\left|x+y+z\right|\ge0\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}2x-1=0\\y-\frac{2}{5}=0\\x+y+z=0\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{2}{5}\\\frac{1}{2}+\frac{2}{5}+z=0\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{2}{5}\\z=-\frac{9}{10}\end{cases}}}\)
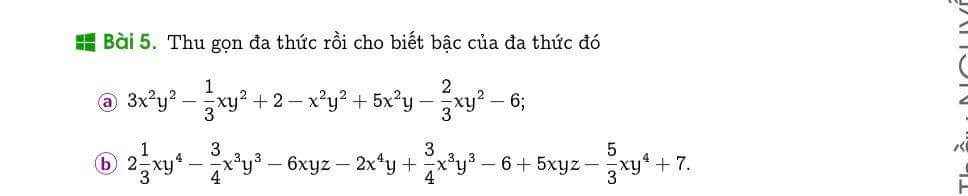 Cứu mik với, mik cảm ơn
Cứu mik với, mik cảm ơn 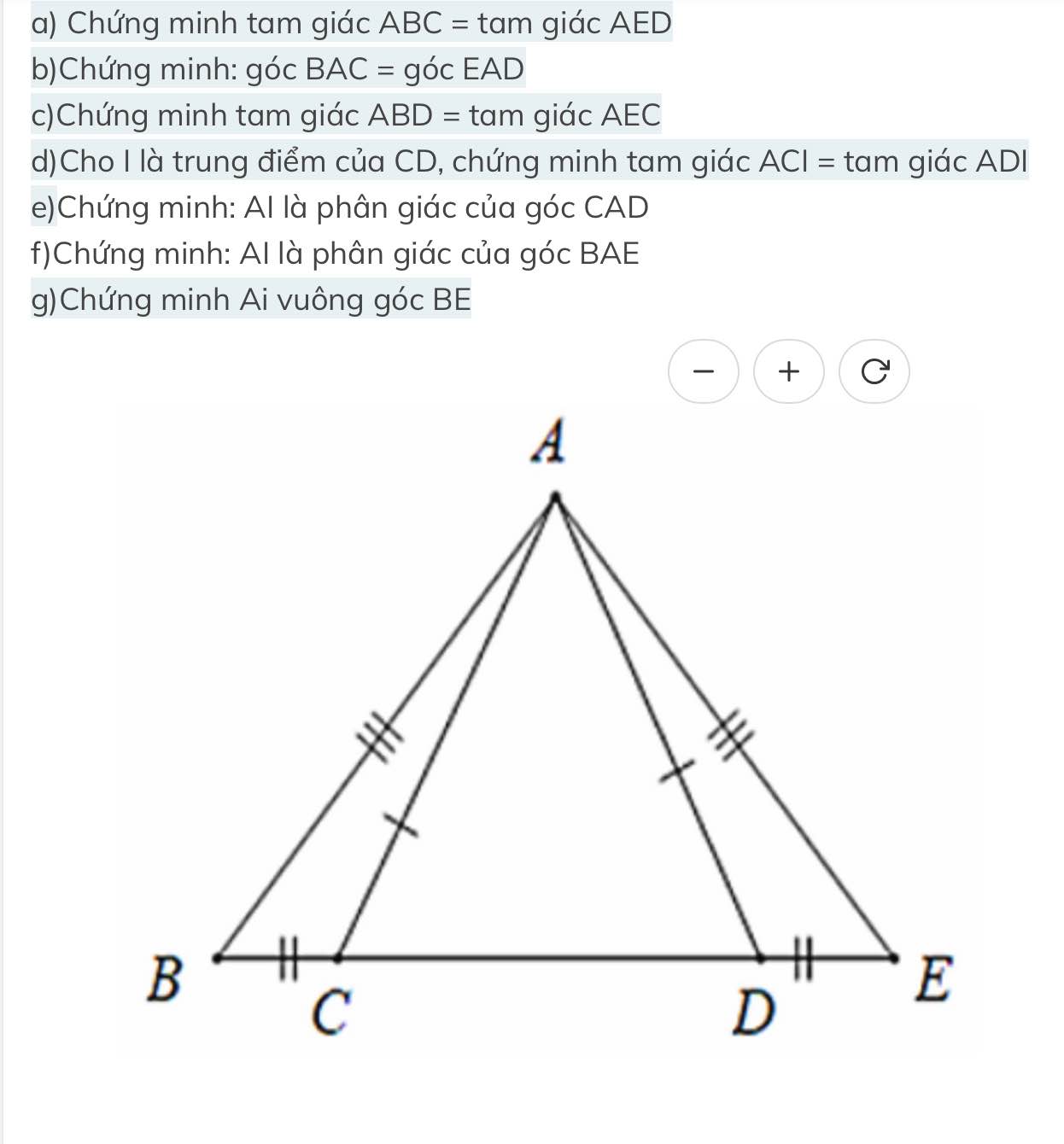
 BÀi hai bỏ đi nhá , bài 1 thôi !!! Chân Thành cảm ơn AE
BÀi hai bỏ đi nhá , bài 1 thôi !!! Chân Thành cảm ơn AE
Để 4-\(|\)5x + 3\(|\)lớn nhất
=>\(|\)5x + 3\(|\)nhỏ nhất
mà \(|\)5x + 3\(|\)\(\ge\)0 với mọi x
<=>5x + 3 = 0
<=>5x = -3
<=>x=\(\frac{-3}{5}\)
<=>D = 4- 0 =4
Vậy GTLN của D là 4 <=>x=\(\frac{-3}{5}\)
\(D=4-|5x+3|\)
Ta có: \(|5x+3|\ge0\Rightarrow4-|5x+3|\le4\)
hay dấu "=" xảy ra khi
\(5x+3=0\)
\(\Leftrightarrow5x=-3\)
\(\Leftrightarrow x=\frac{-3}{5}\)
Vậy GTLN của \(D=4\) khi \(x=\frac{-3}{5}\)